题目内容
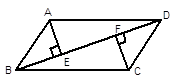
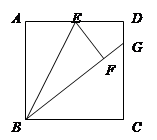
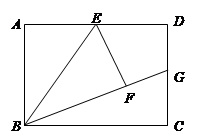
正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.

小题1:求证:△DEF∽△CEB;
小题2:当点P运动到DA的中点时,求证:点F为DC的中点.

小题1:求证:△DEF∽△CEB;
小题2:当点P运动到DA的中点时,求证:点F为DC的中点.
小题1:∵ DE⊥CP,EF⊥BE,
∴ ∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,
∴ ∠1=∠2. ……………………………(2分)
∵ 四边形ABCD是正方形,∴ ∠4+∠6=∠DCB=90°,
在Rt△DEC中,∠4+∠5=90°,
∴ ∠5=∠6, ……………………………(5分)
∴ △DEF∽△CEB. ……………………………(6分)

小题2:∵ 四边形ABCD是正方形,
∴ 当点P运动到DA的中点时,PD=
 AD=
AD= DC.
DC.∴ 在Rt△PDC中,tan∠4=
 ,
,∵ 在Rt△DEC中,tan∠4=
 ,
,∴
 . ……………………………(9分)
. ……………………………(9分)∵ △DEF∽△CEB,
∴
 . ……………………………(11分)
. ……………………………(11分)∵ CB=DC,
∴

∴ 点F为DC的中点. ……………………………(12分)
(注:用其它方法求解参照以上标准给分.)
略

练习册系列答案
相关题目
 是⊙O的直径,点
是⊙O的直径,点 是
是 上任意一点,过点
上任意一点,过点 点
点 是
是 上任一点,连结
上任一点,连结 交
交 于
于 连结AC、CF、BD、OD.
连结AC、CF、BD、OD.
 ;
; 与
与 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想; 的面积与△
的面积与△ 的面积之比为1:2?并加以证明.
的面积之比为1:2?并加以证明.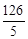 ;
;
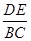 的值小题2: (2)求
的值小题2: (2)求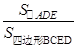 的值
的值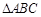 的AB、 AC边上的点,
的AB、 AC边上的点,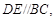
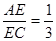 那么
那么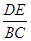 等于(
等于(