题目内容
已知正方形纸片ABCD的边长为2.
操作:如图1,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
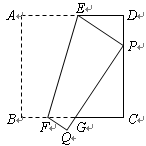
探究:小题1:(1)观察操作结果,找到一个与△DEP相似的三角形,并证明你的结论;
小题2:(2)当点P位于CD中点时,你找到的三角形与△DEP周长的比是多少?
操作:如图1,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.

探究:小题1:(1)观察操作结果,找到一个与△DEP相似的三角形,并证明你的结论;
小题2:(2)当点P位于CD中点时,你找到的三角形与△DEP周长的比是多少?
小题1:(1)
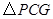 与
与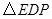 相似.……………1分
相似.……………1分证明:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=
 90°.
90°.由折叠知 ∠EP
 Q=∠A=90°.
Q=∠A=90°.∴∠PED+∠DPE=90°,∠DPE+∠CPG=90°.
 ∴∠PED=∠CPG.
∴∠PED=∠CPG.∴
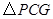 ∽
∽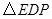 .
.小题2:(2)设ED=x,则AE=
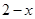 ,
,由
 折叠可知:EP=AE=
折叠可知:EP=AE=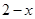 .
.∵点P是CD中点,∴DP=1.
∵∠D=90°,∴
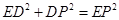 , ……………8分
, ……………8分即
 解得
解得
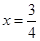 .∴
.∴ .……………………………10分
.……………………………10分∵
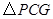 ∽
∽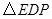 ,∴
,∴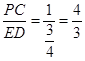 .∴
.∴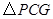 与
与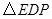 周长的比为4∶
周长的比为4∶ 3
3略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
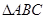 中,点
中,点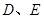 分别在边
分别在边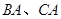 上,
上,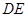 ∥
∥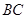 ,
,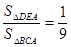 ,
,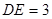 ,那么
,那么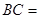 ▲ .
▲ .

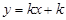 的图象经过点
的图象经过点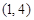 ,且分别与
,且分别与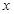 轴、
轴、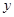 轴交于点
轴交于点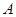 、
、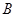 .
.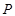
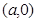 在
在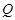
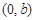 在
在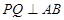 .
.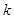 的值,并在给出的平面直角坐标系中画出该一次函数的图象;
的值,并在给出的平面直角坐标系中画出该一次函数的图象;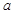 与
与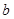 满足的等量关系式.
满足的等量关系式. ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2. E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设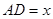 ,
,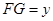 ,
,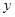 关于
关于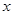 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域; 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,