题目内容
如图,四边形OABC的顶点A(0,4),B(-2,4),C(-4,0).过作B、C直线l,将直线l平移,平移后的直线l与x轴交于D,与y轴交于点E.
探究:当直线l向左或向右平移时(包括直线l与BC直线重合),在直线AB上是否存在P,使△PDE为等腰三角形?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.

探究:当直线l向左或向右平移时(包括直线l与BC直线重合),在直线AB上是否存在P,使△PDE为等腰三角形?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.

由A(0,4),B(-2,4)、C(-4,0)得:OA=4,OC=4,
直线BC:y=2x+8,
又∵BC∥DE,
∴设直线DE的解析式是:y=2x+b,
∴D(-
,0),E(0,b).
∴OD=
b,OE=b.
①如图1、2,以点D为直角顶点,作PP1⊥x轴,
在Rt△ODE中,OE=2OD,
可证Rt△ODE≌Rt△P1PD,
∴OD=PP1=4, DP1=OE=8.
DP1=OE=8.
∴OP1=12,
∴P(-12,4),P(-4,4).
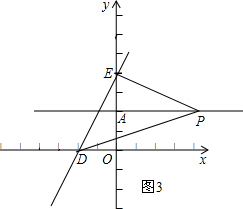
②以点E为直角顶点,如图3,
∴△AEP≌△ODE,
∴AE=OD,OE=AP,
∴AE=
OE,
∴OE=2OA=8,
∴AP=8,
∴P(8,4),
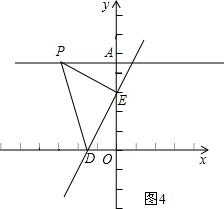
如图4,可以得出△PAE≌△EOD,
∴AE=DO,PA=OE.
∴OE=2AE,
∵AE+OE=4,
∴AE=
,OE=
,
∴PA=
,
∴P(-
,4).
以E为直角顶点,E在O点的下方不存在.
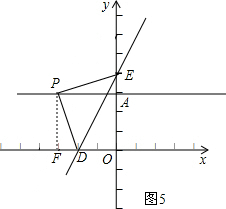
③以P为直角顶点,如图5,作PF⊥x轴于F,
∴易得△PAE≌△PFD,
∴PA=PF=4,
∴P(-4,4);
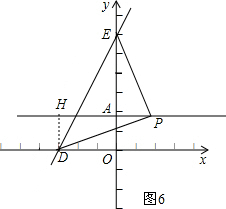
如图6,作DH⊥AB于H,易得出:
△PHD≌△EAP,
∴HD=AP,AE=HP,
∴AE=8,AP=4,
∴P(4,4).
综上所述,P点坐标为:
P1(-12,4),P2(-4,4),P3(8,4),P4(-
,4),P5(4,4).

直线BC:y=2x+8,
又∵BC∥DE,
∴设直线DE的解析式是:y=2x+b,
∴D(-
| b |
| 2 |
∴OD=
| 1 |
| 2 |
①如图1、2,以点D为直角顶点,作PP1⊥x轴,
在Rt△ODE中,OE=2OD,
可证Rt△ODE≌Rt△P1PD,
∴OD=PP1=4,
 DP1=OE=8.
DP1=OE=8.∴OP1=12,
∴P(-12,4),P(-4,4).

②以点E为直角顶点,如图3,
∴△AEP≌△ODE,
∴AE=OD,OE=AP,
∴AE=
| 1 |
| 2 |
∴OE=2OA=8,
∴AP=8,
∴P(8,4),
如图4,可以得出△PAE≌△EOD,
∴AE=DO,PA=OE.
∴OE=2AE,
∵AE+OE=4,
∴AE=
| 4 |
| 3 |
| 8 |
| 3 |
∴PA=
| 8 |
| 3 |
∴P(-
| 8 |
| 3 |
以E为直角顶点,E在O点的下方不存在.


③以P为直角顶点,如图5,作PF⊥x轴于F,
∴易得△PAE≌△PFD,
∴PA=PF=4,
∴P(-4,4);
如图6,作DH⊥AB于H,易得出:
△PHD≌△EAP,
∴HD=AP,AE=HP,
∴AE=8,AP=4,
∴P(4,4).
综上所述,P点坐标为:
P1(-12,4),P2(-4,4),P3(8,4),P4(-
| 8 |
| 3 |


练习册系列答案
相关题目

 BP交⊙P于点C
BP交⊙P于点C


 B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).
B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动). 单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.