题目内容
如图,已知点A、B分别在x轴、y轴上,AB=12,∠OAB=30°,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个 单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
(1)直接写出A、B点坐标是A点______,B点______;
(2)用含t的代数式求出表示点P的坐标;
(3)过O作OC⊥l于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并写出此时⊙P与直线CD的位置关系.
 单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.(1)直接写出A、B点坐标是A点______,B点______;
(2)用含t的代数式求出表示点P的坐标;
(3)过O作OC⊥l于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并写出此时⊙P与直线CD的位置关系.
(1)在Rt△OAB中,AB=12,∠OAB=30°,
∴OB=6(30°所对的直角边是斜边的一半),
OA=6
(勾股定理),
∴A(6
,0),B(0,6);
(2)作PF⊥y轴于F.
∵∠BAO=30°.
∴在直角三角形PFB′中,PB′=t,∠B′PF=30°,
则B′F=
,PF=
t.
又BB′=t,
∴OF=OB-BB′-B′F=6-t-
=6-
t,
则P点的坐标为(
t,6-
t).
(3)此题应分为两种情况:
①当⊙P和OC第一次相切时,
设直线B′P与OC的交点是M.
根据题意,知∠BOC=∠BAO=30°.
则B′M=
OB′=3-
,
∵PB′=t
∴PM=B′M-PB′=3-
t.
根据直线和圆相切,则圆心到直线的距离等于圆的半径,得
3-
t=1,t=
.
此时⊙P与直线CD显然相离;
②当⊙P和OC第二次相切时,
则有
t-3=1,t=
.
此时⊙P与直线CD显然相交.
答:当t=
或
时⊙P和OC相切,t=
时⊙P和直线CD相离,当t=
时⊙P和直线CD相交.

∴OB=6(30°所对的直角边是斜边的一半),
OA=6
| 3 |
∴A(6
| 3 |
(2)作PF⊥y轴于F.
∵∠BAO=30°.
∴在直角三角形PFB′中,PB′=t,∠B′PF=30°,
则B′F=
| t |
| 2 |
| ||
| 2 |

又BB′=t,
∴OF=OB-BB′-B′F=6-t-
| t |
| 2 |
| 3 |
| 2 |
则P点的坐标为(
| ||
| 2 |
| 3 |
| 2 |
(3)此题应分为两种情况:
①当⊙P和OC第一次相切时,
设直线B′P与OC的交点是M.
根据题意,知∠BOC=∠BAO=30°.
则B′M=
| 1 |
| 2 |
| t |
| 2 |
∵PB′=t
∴PM=B′M-PB′=3-
| 3 |
| 2 |

根据直线和圆相切,则圆心到直线的距离等于圆的半径,得
3-
| 3 |
| 2 |
| 4 |
| 3 |
此时⊙P与直线CD显然相离;
②当⊙P和OC第二次相切时,
则有
| 3 |
| 2 |
| 8 |
| 3 |
此时⊙P与直线CD显然相交.
答:当t=
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |


练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根. 信息,解答下列问题:
信息,解答下列问题:
 示.求:
示.求: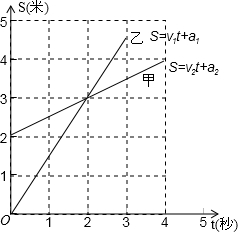

 圆心的圆的半径为1.
圆心的圆的半径为1.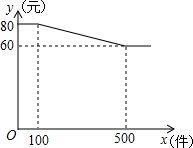 数关系如图所示.
数关系如图所示.