题目内容
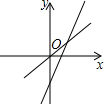
如图,P是y轴上一动点,是否存在平行于y轴的直线x=t,使它与直线y=x和直线y=-
x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.

| 1 |
| 2 |

存在.
方法一:当x=t时,y=x=t;
当x=t时,y=-
x+2=-
t+2.
∴E点坐标为(t,-
t+2),D点坐标为(t,t).(2分)
∵E在D的上方,
∴DE=-
t+2-t=-
t+2,且t<
.(3分)
∵△PDE为等腰直角三角形,
∴PE=DE或PD=DE或PE=PD.(4分)
若t>0,PE=DE时,-
t+2=t,
∴t=
,-
t+2=
,
∴P点坐标为(0,
).(5分)
若t>0,PD=DE时,-
t+2=t,
∴t=
,
∴P点坐标为(0,
).(6分)
若t>0,PE=PD时,即DE为斜边,
∴-
t+2=2t(7分)
∴t=
,DE的中点坐标为(t,
t+1),
∴P点坐标为(0,
).(8分)
若t<0,PE=DE和PD=DE时,由已知得DE=-t,-
t+2=-t,t=4>0(不符合题意,舍去),
此时直线x=t不存在.(10分)
若t<0,PE=PD时,即DE为斜边,由已知得DE=-2t,-
t+2=-2t,(11分)
∴t=-4,
t+1=0,
∴P点坐标为(0,0).(12分)
综上所述:当t=
时,△PDE为等腰直角三角形,此时P点坐标为(0,
)或(0,
);
当t=
时,△PDE为等腰直角三角形,此时P点坐标为(0,
);
当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
方法二:设直线y=-
x+2交y轴于点A,交直线y=x于点B,过B点作BM垂直于y轴,垂足为M,交DE于点N.
∵x=t平行于y轴,
∴MN=|t|.(1分)
∵
,
解得x=
,y=
,
∴B点坐标为(
,
),
∴BM=
,
当x=0时,y=-
x+2=2,
∴A点坐标为(0,2),
∴OA=2.(3分)
∵△PDE为等腰直角三角形,
∴PE=DE或PD=DE或PE=PD.(4分)
如图,若t>0,PE=DE和PD=DE时,
∴PE=t,PD=t,
∵DE∥OA,
∴△BDE∽△BOA,
∴
=
.(5分)
∴
=
,
∴t=
当t=
时,y=-
x+2=
,y=x=
∴P点坐标为(0,
)或(0,
).(6分)
若t>0,PD=PE时,即DE为斜边,
∴DE=2MN=2t.
∵DE∥OA,
∴△BDE∽△BOA,
∴
=
(7分)
∴
=
,
∴MN=t=
,DE中点的纵坐标为
t+1=
,
∴P点坐标为(0,
)(8分)
如图,
若t<0,PE=DE或PD=DE时,
∵DE∥OA,
∴△BDE∽△BOA,
∴
=
(9分)
DE=-4(不符合题意,舍去),此时直线x=t不存在.(10分)
若t<0,PE=PD时,即DE为斜边,
∴DE=2MN=-2t,
∵DE∥OA,
∴△BDE∽△BOA,
∴
=
(11分)
∴
=
,
∴MN=4,
∴t=-4,
t+1=0,
∴P点坐标为(0,0).(12分)
综上述所述:当t=
时,△PDE为等腰直角三角形,此时P点坐标为(0,
)或(0,
);
当t=
时,△PDE为等腰直角三角形,此时P点坐标为(0,
);当t=-4时,
△PDE为等腰直角三角形,此时P点坐标为(0,0).
方法一:当x=t时,y=x=t;
当x=t时,y=-
| 1 |
| 2 |
| 1 |
| 2 |

∴E点坐标为(t,-
| 1 |
| 2 |
∵E在D的上方,
∴DE=-
| 1 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
∵△PDE为等腰直角三角形,
∴PE=DE或PD=DE或PE=PD.(4分)
若t>0,PE=DE时,-
| 3 |
| 2 |
∴t=
| 4 |
| 5 |
| 1 |
| 2 |
| 8 |
| 5 |
∴P点坐标为(0,
| 8 |
| 5 |
若t>0,PD=DE时,-
| 3 |
| 2 |
∴t=
| 4 |
| 5 |
∴P点坐标为(0,
| 4 |
| 5 |
若t>0,PE=PD时,即DE为斜边,
∴-
| 3 |
| 2 |
∴t=
| 4 |
| 7 |
| 1 |
| 4 |
∴P点坐标为(0,
| 8 |
| 7 |
若t<0,PE=DE和PD=DE时,由已知得DE=-t,-
| 3 |
| 2 |
此时直线x=t不存在.(10分)
若t<0,PE=PD时,即DE为斜边,由已知得DE=-2t,-
| 3 |
| 2 |
∴t=-4,
| 1 |
| 4 |
∴P点坐标为(0,0).(12分)
综上所述:当t=
| 4 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
当t=
| 4 |
| 7 |
| 8 |
| 7 |
当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
方法二:设直线y=-
| 1 |
| 2 |

∵x=t平行于y轴,
∴MN=|t|.(1分)
∵
|
解得x=
| 4 |
| 3 |
| 4 |
| 3 |
∴B点坐标为(
| 4 |
| 3 |
| 4 |
| 3 |
∴BM=
| 4 |
| 3 |
当x=0时,y=-
| 1 |
| 2 |
∴A点坐标为(0,2),
∴OA=2.(3分)
∵△PDE为等腰直角三角形,
∴PE=DE或PD=DE或PE=PD.(4分)
如图,若t>0,PE=DE和PD=DE时,
∴PE=t,PD=t,
∵DE∥OA,
∴△BDE∽△BOA,
∴
| DE |
| OA |
| BN |
| BM |
∴
| t |
| 2 |
| ||
|
∴t=
| 4 |
| 5 |
当t=
| 4 |
| 5 |
| 1 |
| 2 |
| 8 |
| 5 |
| 4 |
| 5 |
∴P点坐标为(0,
| 8 |
| 5 |
| 4 |
| 5 |
若t>0,PD=PE时,即DE为斜边,
∴DE=2MN=2t.
∵DE∥OA,
∴△BDE∽△BOA,
∴
| DE |
| OA |
| BN |
| BM |
∴
| 2MN |
| 2 |
| ||
|
∴MN=t=
| 4 |
| 7 |
| 1 |
| 4 |
| 8 |
| 7 |
∴P点坐标为(0,
| 8 |
| 7 |
如图,
若t<0,PE=DE或PD=DE时,
∵DE∥OA,
∴△BDE∽△BOA,
∴
| DE |
| OA |
| BN |
| BM |
DE=-4(不符合题意,舍去),此时直线x=t不存在.(10分)
若t<0,PE=PD时,即DE为斜边,
∴DE=2MN=-2t,
∵DE∥OA,
∴△BDE∽△BOA,
∴
| DE |
| OA |
| BN |
| BM |
∴
| 2MN |
| 2 |
| ||
|
∴MN=4,
∴t=-4,
| 1 |
| 4 |
∴P点坐标为(0,0).(12分)
综上述所述:当t=
| 4 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
当t=
| 4 |
| 7 |
| 8 |
| 7 |
△PDE为等腰直角三角形,此时P点坐标为(0,0).

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根. 信息,解答下列问题:
信息,解答下列问题:





 数关系如图所示.
数关系如图所示.