题目内容
如图,直线y=-
x+6与x,y轴分别交于点A,C,过点A、C分别作x,y轴的垂线,交于点B,点D为AB的中点.点P从点A出发,以每秒1个单位的速度,沿△AOC边A→O→C→A的方向运动,运动时间为t(秒).
(1)求点B的坐标;
(2)设△APC的面积为S,求S关于t的函数解析式;
(3)在点P的运动过程中,是否存在点P,使△ADP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

| 3 |
| 4 |
(1)求点B的坐标;
(2)设△APC的面积为S,求S关于t的函数解析式;
(3)在点P的运动过程中,是否存在点P,使△ADP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

(1)∵直线y=-
x+6与x,y轴分别交于点A,C,
∴点A的坐标为:(8,0),点C的坐标为:(0,6),
∵过点A、C分别作x,y轴的垂线,交于点B,
∴点B的坐标为:(8,6);
(2)当0≤t≤8时,点P在OA上,
∵AP=t,OC=6,
∴S=
AP•OC=
×t×6=3t;
当8<t<14时,点P在OC上,
∵PC=OA+OC-t=14-t,OA=8,
∴S=
PC•OA=
×(14-t)×8=-4t+56;
 (3)存在.
(3)存在.
∵点D为AB的中点,
∴AD=
AB=3,
①当0≤t≤8时,点P在OA上,
∵∠OAD=90°,
∴当AP=AD=3时,
∴t=3;
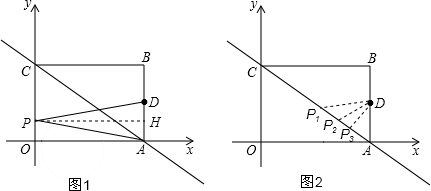
②如图1,当8<t≤14时,点P在OC上,
过点P作PH⊥AB于点H,
∵PA=PD,
∴AH=
AD=1.5,
∴OP=AH=1.5,
∴t=9.5;
③如图2,当14<t≤24时,点P在AC上,
当AD=P1D时,AP1=2AD•cos∠BAC=3.6,
∴t=OA+OC+AC-AP1=24-3.6=20.4;
当AP2=AD=3时,t=24-3=21;
当AP3=P3D时,AP3=2.5,
∴t=24-2.5=21.5.
综上可得:t=3或t=9.5或t=20.4或t=21或t=21.5.
| 3 |
| 4 |
∴点A的坐标为:(8,0),点C的坐标为:(0,6),
∵过点A、C分别作x,y轴的垂线,交于点B,
∴点B的坐标为:(8,6);
(2)当0≤t≤8时,点P在OA上,
∵AP=t,OC=6,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
当8<t<14时,点P在OC上,
∵PC=OA+OC-t=14-t,OA=8,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
 (3)存在.
(3)存在.∵点D为AB的中点,
∴AD=
| 1 |
| 2 |
①当0≤t≤8时,点P在OA上,
∵∠OAD=90°,
∴当AP=AD=3时,
∴t=3;
②如图1,当8<t≤14时,点P在OC上,
过点P作PH⊥AB于点H,
∵PA=PD,
∴AH=
| 1 |
| 2 |
∴OP=AH=1.5,
∴t=9.5;
③如图2,当14<t≤24时,点P在AC上,
当AD=P1D时,AP1=2AD•cos∠BAC=3.6,
∴t=OA+OC+AC-AP1=24-3.6=20.4;
当AP2=AD=3时,t=24-3=21;
当AP3=P3D时,AP3=2.5,
∴t=24-2.5=21.5.
综上可得:t=3或t=9.5或t=20.4或t=21或t=21.5.

练习册系列答案
相关题目


 示.求:
示.求: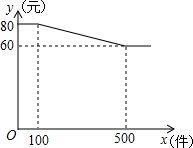 数关系如图所示.
数关系如图所示.


