题目内容
解答题:如图,⊙P与x轴相切于坐标原点O,⊙P与y轴交于点A(0,2),点B的坐标为(-2
,0),连接 BP交⊙P于点C
BP交⊙P于点C
(1)求线段BC的长;
(2)求直线AC的函数解析式.
| 2 |
 BP交⊙P于点C
BP交⊙P于点C(1)求线段BC的长;
(2)求直线AC的函数解析式.
(1)∵⊙P与x轴切于坐标原点O,且交y轴于点A(0,2),
∴AO⊥x轴于O,OA是直径且OA=2,
∴OP=1,
又∵BP交⊙P于C,∴CP=1,
∵B(-2
,0),∴OB=2
,
Rt△BOP中,根据勾股定理得:BP=
=3,
则BC=BP-CP=2;
(2)过C作CH⊥BO于H,
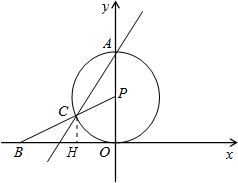
∵AO⊥x轴,
∴CH∥PO,
∴
=
=
,
又∵PO=1,BC=2,BP=3,OB=2
,
∴CH=
=
,BH=
=
,
∴HO=OB-BH=
,
∴C(-
,
),
根据直线AC交y轴于点A(0,2),设直线AC的解析式为y=kx+2(k≠0),
将C的坐标代入得:-
k+2=
,
∴k=
,
∴直线AC的解析式为y=
x+2.
∴AO⊥x轴于O,OA是直径且OA=2,
∴OP=1,
又∵BP交⊙P于C,∴CP=1,
∵B(-2
| 2 |
| 2 |
Rt△BOP中,根据勾股定理得:BP=
(2
|
则BC=BP-CP=2;
(2)过C作CH⊥BO于H,
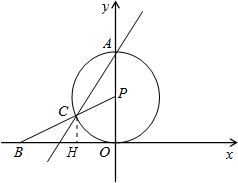
∵AO⊥x轴,
∴CH∥PO,
∴
| CH |
| PO |
| BC |
| BP |
| BH |
| BO |
又∵PO=1,BC=2,BP=3,OB=2
| 2 |
∴CH=
| PO•BC |
| BP |
| 2 |
| 3 |
| CH•BO |
| PO |
| 4 |
| 3 |
| 2 |
∴HO=OB-BH=
| 2 |
| 3 |
| 2 |
∴C(-
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
根据直线AC交y轴于点A(0,2),设直线AC的解析式为y=kx+2(k≠0),
将C的坐标代入得:-
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
∴k=
| 2 |
∴直线AC的解析式为y=
| 2 |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目








 距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题:
距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题: