题目内容
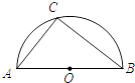
【题目】△ABC中,AD是BC边上的高,BD=3,CD=1,AD=2,P、Q、R分别是BC、AB、AC边上的动点,则△PQR周长的最小值为 .
【答案】![]()
【解析】如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,
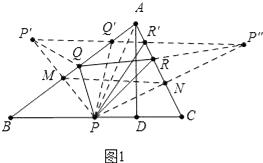
此时△PQ′R′的周长最小,这个最小值=P′P″,
∵PM=MP′,PN=NP″,
∴P′P″=2MN,
∴当MN最小时P′P″最小.如图2中,
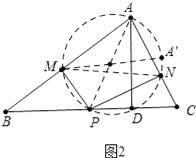
∵∠AMP=∠ANP=90°,
∴A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,
∵∠MAN是定值,
∴直径AP最小时,弦MN最小,
∴当点P与点D重合时,PA最小,此时MN最小.
如图3中,

∵在RT△ABD中,∠ADB=90°,AD=2,DB=3,
∴AB= ![]() ,在RT△ADC中,
,在RT△ADC中,
∵∠ADC=90°,AD=2,CD=1,
∴AC= ![]() ,
,
∵DM⊥AB,DN⊥AC,
∴ ![]() ACDN=
ACDN= ![]() DCAD,
DCAD,
∴DN= ![]() ,AN=
,AN= ![]() ,
,
∵∠MAD=∠DAB,∠AMD=∠ADB,
∴△AMD∽△ADB,∴ ![]() ,
,
∴ ![]() =AMAB,同理
=AMAB,同理 ![]() =ANAC,
=ANAC,
∴AMAB=ANAC,
∴ ![]() ,
,
∵∠MAN=∠CAB,∴△AMN∽△ACB,
∴ ![]() ,
,
∴ ![]() ,
,
∴MN= ![]() ,
,
∴△PQR周长的最小值=P′P″=2MN= ![]() .
.
故答案为: ![]() .
.
如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,此时△PQ′R′的周长最小,这个最小值=P′P″,然后证出P′P″=2MN,当MN最小时P′P″最小.如图2中, 根据圆周角定理得出A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,又由于∠MAN是定值,故直径AP最小时,弦MN最小,从而知道当点P与点D重合时,PA最小,此时MN最小,如图3中,首先根据勾股定理得出AB,AC的长度,然后根据面积法得出DN长,再根据勾股定理算出AN的长,进而判断出△AMD∽△ADB,根据相似三角形的性质得出 A D 2 =AMAB,同理 A D 2 =ANAC,故AMAB=ANAC,从而再判断出△AMN∽△ACB,根据相似三角形的性质得出MN的长,从而得出答案。