题目内容
【题目】计算或方程：
（1）3（x﹣4）3﹣1536＝0；
（2）3
﹣（
﹣2）；
（3）
（用代入法）；
（4）
．
【答案】（1）x＝12；（2）5
﹣
；（3）
；（4）
．
【解析】
（1）首先把1536移到等号右边，等式两边再除以3，然后再求立方根可得答案；
（2）首先去括号，然后再算加减即可；
（3）把①变形为y＝2x5③，把③代入②可消去未知数y，解出x的值，然后把x的值代入③可得y的值，进而可得方程组的解；
（4）利用①×3＋②×2减法消元可消去未知数y，解出x的值，然后把x的值代入②可得y的值，进而可得方程组的解．
（1）3（x﹣4）3﹣1536＝0，
3（x﹣4）3＝1536，
（x﹣4）3＝512，
x﹣4＝8，
x＝12；
（2）原式＝3﹣+2＝5﹣；
（3）
，
由①得：y＝2x﹣5③，
把③代入②得：3x+4（2x﹣5）＝2，
解得：x＝2，
把x＝2代入③得：y＝﹣1，
∴方程组的解为：；
（4）
，
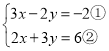①×3+②×2得：x＝
，
把x＝代入②得：2×+3y＝6，
解得：y＝
，
∴方程组的解为：．
【题目】某童装店有A、B两种型号的童装，其进价与售价如下表所示：
型号 | 进价（元） | 售价（元） |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要，服装店决定：购进A种服装的数量要比购进B种服装的2倍还多4件，且A种服装购进数量不超过28件，并使这批服装全部销售完毕后的总利润不少于699元．若假设购进B种服装x件，那么：
（1）请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示；
（2）请问该服装店有几种满足条件的进货方案？哪种方案获利最多？
【题目】已知A、B在数轴上分别表示a、b
（1）对照数轴填写下表：
a | 6 | -6 | -6 | -6 | -10 | -2.5 |
b | 4 | 0 | 4 | -4 | 2 | -2.5 |
两点距离 | 2 | 6 | 0 |
（2）若A、B两点间的距离记为 d，试问d与a、b有何数量关系；
（3）在数轴上找到所有符合条件的整数点P，使它到5和﹣5的距离之和为10，并求出所有这些整数的和；
（4）若数轴上点C表示的数为x，当点C在什么位置时，
①|x+1|的值最小；②|x+1|+|x﹣2|的值最小．
