Question

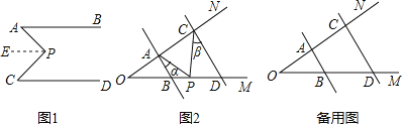
【题目】如图，在平面直角坐标系中，直线与x轴，y轴分别交于点A，B，将沿过点A的直线折叠，使点B落在x轴的负半轴上，记作点C，折痕与y轴交于点D，则点D的坐标为______．

Answer 1

【答案】

【解析】

由条件可先求得A、B坐标．在Rt△AOB中，可求得AB，进而求得OC，设OD=x，则可表示出CD．在Rt△COD中，由勾股定理可列方程，可求得x的值，即可求得D点坐标．

在yx+2中，令y=0可求得：x=4，令x=0可求得：y=2，∴A点坐标为（4，0），B点坐标为（0，2），∴OA=4，OB=2．

在Rt△AOB中，由勾股定理可得：AB6，又将△AOB沿过点A的直线折叠B与C重合，∴AC=AB=6，BD=CD，∴OC=AC﹣OA=6﹣4=2．

设OD=x，则BD=CD=2x．

在Rt△OCD中，由勾股定理可得：CD2=OC2+OD2，∴（2x）2=x2+22，解得：x，∴D点坐标为（0，）．

故答案为：（0，）．