题目内容
【题目】已知:在梯形ABCD中,AD//BC,AC=BC=10,![]() ,点E在对角线AC上,且CE=AD,BE的延长线与射线AD、射线CD分别相交于点F、G.设AD=x,△AEF的面积为y.
,点E在对角线AC上,且CE=AD,BE的延长线与射线AD、射线CD分别相交于点F、G.设AD=x,△AEF的面积为y.
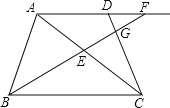
(1)求证:∠DCA=∠EBC;
(2)如图,当点G在线段CD上时,求y关于x的函数解析式,并写出它的定义域;
(3)如果△DFG是直角三角形,求△AEF的面积.
【答案】(1)见解析;(2)![]() ,
,![]() ;(3)15或
;(3)15或![]() .
.
【解析】
(1)由AD与BC平行,得到一对内错角相等,再由AD=CE,AC=BC,利用SAS可得△DCA≌△ECB,由全等三角形的性质可得结论;
(2)由AD与BC平行,得到三角形AEF与三角形CEB相似,由相似得比例表示出AF,过E作EH垂直于AF,根据锐角三角函数定义表示出EH,进而表示出y与x的函数解析式,并求出x的范围即可;
(3)分两种情况考虑:①当∠FDG=90°时,如图2所示,在直角三角形ACD中,利用锐角三角函数定义求出AD的长,即为x的值,代入求出y的值,即为三角形AEF面积;②当∠DGF=90°时,过E作EM⊥BC于点M,如图3所示,由相似列出关于x的方程,求出方程的解得到x的值,进而求出y的值,即为三角形AEF面积.
解:(1)证明:∵AD∥BC,
∴∠DAC=∠ECB,
在△DCA和△ECB中,
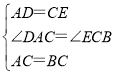 ,
,
∴△DCA≌△ECB(SAS),
∴∠DCA=∠EBC;
(2)∵AD∥BC,
∴△AEF∽△CEB,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
作EH⊥AF于H,如图1所示,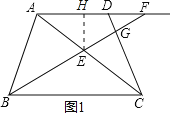
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∵点G在线段CD上,
∴AF≥AD,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴y关于x的函数解析式为:![]() ,定义域为
,定义域为![]() .
.
(3)(3)分两种情况考虑:
①当∠FDG=90°时,如图2所示:
在Rt△ADC中,![]() ,即
,即![]() ,
,
∴![]() ;
;
②当∠DGF=90°时,过E作EM⊥BC于点M,如图3所示,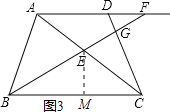
由(1)得:CE=AD=x,
在Rt△EMC中,![]() ,
,![]() ,
,
∴![]() ,
,
∵∠GCE=∠GBC,∠EGC=∠CGB,
∴△CGE∽△BGC,
∴![]() ,即
,即![]() ,
,
∵∠EBM=∠CBG,∠BME=∠BGC=90°,
∴△BME∽△BGC,
∴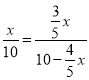 ,即
,即![]() ,
,
此时![]() ,
,
∴综上,此时△AEF的面积为![]() 或15.
或15.