题目内容
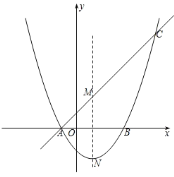
【题目】如图,抛物线![]() 交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
(1)求抛物线的函数关系式;
(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;
(3)在(2)的条件下,求△AQC面积的最大值.
【答案】(1)![]() ;(2)PQ有最大值=
;(2)PQ有最大值=![]() ,此时P(2,3);(3)
,此时P(2,3);(3)![]()
【解析】
(1)由于点M和抛物线顶点关于x轴对称,即可得到点N的坐标,进而表示出该抛物线的顶点坐标式函数解析式;
(2)将点A与点M的坐标代入y=kx+b求出k与b的值,确定直线AC的解析式,得到点P坐标为(x,x+1),根据直线AC和抛物线的解析式,即可得到P、Q的纵坐标,从而得到关于PQ的长和P点横坐标的函数关系式,根据所得函数的性质即可求出PQ的最大值及对应的P点坐标;
(3)由于△AQC面积=△AQP面积+△CPQ面积,根据三角形面积公式将PQ的最大值代入计算即可求解.
(1)由题意知,抛物线顶点N的坐标为(1,-2),
![]()
(2)由(1)![]() 得:x=-1或3,即A(-1,0)、B(3,0);
得:x=-1或3,即A(-1,0)、B(3,0);
∵将A(-1,0)、M(1,2)代入y=kx+b中得:![]()
解得:![]()
∴直线AC的函数关系式为y=x+1,
解方程组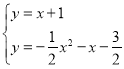
得x=-1或5,即A(-1,0)、C(5,6);
![]()
∴点P在线段AC之间
设P坐标为(x,x+1),则Q的坐标为![]()
∴PQ=(x+1) - (![]() )=
)= ![]()
![]() 时
时
![]() 有最大值
有最大值![]()
此时![]()
(3)![]()

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目