题目内容
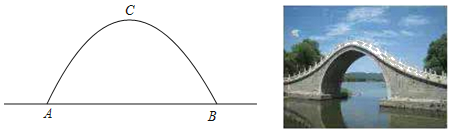
【题目】秋风送爽,学校组织同学们去颐和园秋游,昆明湖西堤六桥中的玉带桥最是令人喜爱,如图所示,玉带桥的桥拱是抛物线形水面宽度AB=10m,桥拱最高点C到水面的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一艘游船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,通过计算说明这艘游船能否安全通过玉带桥.
【答案】(1)图详见解析,y=﹣![]() x2+6;(2)这艘游船能否安全通过玉带桥.
x2+6;(2)这艘游船能否安全通过玉带桥.
【解析】
(1)以AB的中点为原点,建立如下的坐标系,则点C(0,6),点B(5,0),设函数的表达式为:y=ax2+c=ax2+6,即可求解;
(2)设船桥的中心进入,则其最右侧点的横坐标为:2,当x=2时,y=﹣![]() x2+6=﹣
x2+6=﹣![]() ×4+6=
×4+6=![]() =5.04,4.5<5.04,故边沿可以安全通过,此时船的顶部高为4.5,4.5+0.5=5<6,故顶部通过符合要求,即可求解.
=5.04,4.5<5.04,故边沿可以安全通过,此时船的顶部高为4.5,4.5+0.5=5<6,故顶部通过符合要求,即可求解.
解:(1)以AB的中点为原点,建立如下的坐标系,
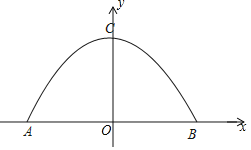
则点C(0,6),点B(5,0),
设函数的表达式为:y=ax2+c=ax2+6,
将点B的坐标代入上式得:0=25a+6,解得:a=﹣![]() ,
,
故抛物线的表达式为:y=﹣![]() x2+6;
x2+6;
(2)设船桥的中心进入,则其最右侧点的横坐标为:2,
当x=2时,y=﹣![]() x2+6=﹣
x2+6=﹣![]() ×4+6=
×4+6=![]() =5.04,
=5.04,
4.5<5.04,故边沿可以安全通过,
此时船的顶部高为4.5,4.5+0.5=5<6,故顶部通过符合要求,
故这艘游船能否安全通过玉带桥.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目