题目内容
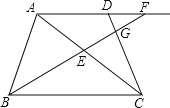
【题目】如图:平行四边形ABCD中,E为AB中点,![]() ,连E、F交AC于G,则AG:GC=______________;
,连E、F交AC于G,则AG:GC=______________;

【答案】1:5
【解析】
延长FE交CB的延长线于M,利用已知条件证明△AFE≌△BME,可得到AF=BM,再有平行线四边形的性质可证明△AFG∽△CMG,利用相似三角形的性质即可求出AG:GC的值.
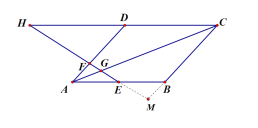
解:延长FE交CB的延长线于M,
∵四边形ABCD是平行四边形,
∴∠EAF=∠MBE,∠AFE=∠BME,
又∵AE=BE,
∴△AFE≌△BME(AAS),
∴AF=BM,
∵AF:FD=1:3,
∴AF:AD=1:4,
∴AF:MC=1:5,
∵AD∥BC,
∴△AFG∽△CMG,
∴AF:MC=AG:GC=1:5,
故答案为:1:5.

练习册系列答案
相关题目