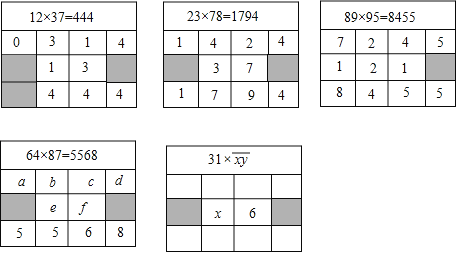
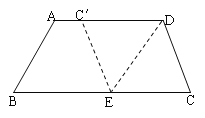
题目内容
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
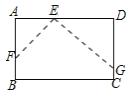
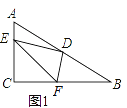
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
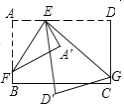
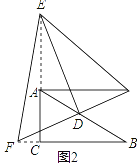
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
【答案】(1)结论:AE2+BF2=EF2 ,理由详见解析;(2) 结论不变, AE2+BF2=EF2,证明详见解析.
【解析】
(1)结论:AE2+BF2=EF2.如图1中,延长FD到M,使得DM=DF,连接AM,EM.首先证明△ADM≌△BDF,得到AM=FB,再证明△AEM是直角三角形,理由勾股定理即可解决问题.
(2)结论不变,证明方法类似(1).
(1)结论:AE2+BF2=EF2 .
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.

在△ADM和△BDF中,
 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .
(2)如图2中,结论不变.AE2+BF2=EF2

理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案