Question

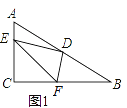
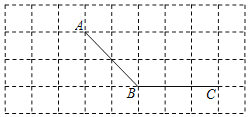
【题目】已知，，按如图1所示摆放，将OA、OC边重合在直线MN上，OB、OD边在直线MN的两侧；

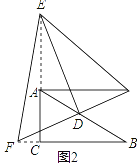
(1)保持不动，将绕点O旋转至如图2所示的位置，则①= ；②= ；

(2)若按每分钟的速度绕点O逆时针方向旋转，按每分钟的速度也绕点O逆时针方向旋转，OC旋转到射线ON上时都停止运动，设旋转t分钟，计算(用t的代数式表示)。

(3)保持不动，将绕点O逆时针方向旋转，若射线OE平分，射线OF平分，求的大小；

Answer 1

【答案】(1)①150°；②30°；(2) 8t－60或2t+60；(3) ∠EOF的大小为15°或165°.

【解析】

（1）①根据∠AOB及∠COD的度数求出∠AOB+∠COD的度数，然后利用角与角之间的关系进行代换化简即可；

②根据∠AOB及∠COD的度数求出∠AOB－∠COD的度数，然后利用角与角之间的关系进行代换化简即可；

（2）分情况讨论：OD与OA相遇前及OD与OA相遇后，画出图形，再根据角与角之间的关系进行计算即可；

（3）分情况讨论，根据角与角之间的关系进行计算即可.

解：(1)①∵∠AOB=90°，∠COD=60°，

∴∠AOB+∠COD=90°+60°=150°，

∵∠AOB=∠AOC+∠BOC，∠COD=∠AOC+∠AOD，

∴∠AOC+∠BOC+∠AOC+∠AOD=150°，

∴∠AOC+∠BOD=150°；

②∵∠AOB=90°，∠COD=60°，

∴∠AOB－∠COD=90°－60°=30°，

∵∠AOB=∠AOC+∠BOC，∠COD=∠AOC+∠AOD，

∴∠AOC+∠BOC－(∠AOC+∠AOD)=30°，

∴∠BOC－∠AOD=30°；

(2)设运动时间为t秒，由题意可知：0<t≤36，∠MOC=5t，∠MOA=2t，

当OD与OA相遇时，5t－2t=60，解得：t=20，

∴经过20秒，OD与OA相遇，

①0<t≤20时，OD与OA相遇前，如图所示，

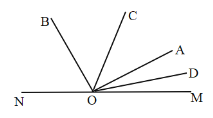
∠AOD=∠COD+∠AOM－∠MOC=60+2t－5t=60－3t，

∴∠MOC－∠AOD=5t－(60－3t)=8t－60；

②20<t≤36时，OD与OA相遇后，如图所示，

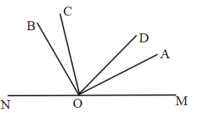
∠AOD=∠MOC－∠COD－∠AOM=5t－60－2t=3t－60，

∴∠MOC－∠AOD=5t－(3t－60)=2t+60；

(3)设OC绕点O逆时针旋转n°，则OD也绕点O逆时针旋转n°，

①0<n°≤150°时，射线OE、OF在射线OB同侧，在直线MN同侧，

∵∠BOD=150°－n°，∠AOC=n°，OE平分∠AOC，OF平分∠BOD，

∴∠BOF=(150°－n°)，∠BOE=90°－n°，

∴∠EOF=∠BOE－∠BOF=15°；

②150°<n°≤180°时，射线OE、OF在射线OB异侧，在直线MN同侧，

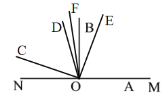
∵∠BOD= n°－150°，∠AOC=n°，OE平分∠AOC，OF平分∠BOD，

∴∠BOF=(n°－150°)，∠BOE=90°－n°，

∴∠EOF=∠BOE+∠BOF=15°；

③180°<n°≤330°时，射线OE、OF在射线OB异侧，在直线MN异侧，

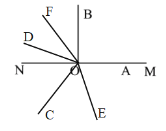
∵∠BOD= n°－150°，∠AOC=360°－n°，OE平分∠AOC，OF平分∠BOD，

∴∠DOF=(n°－150°)，∠COE=(360°－n°)，

∴∠EOF=∠DOF+∠COD+∠COE=165°；

④330°<n°≤360°时，射线OE、OF在射线OB同侧，在直线MN异侧，

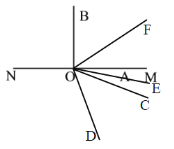
∵∠BOD=360°－(n°－150°)，∠AOC=360°－n°，OE平分∠AOC，OF平分∠BOD，

∴∠DOF=[360°－(n°－150°)]，∠COE=(360°－n°)，

∴∠EOF=∠DOF－∠COD－∠COE=15°；

综上，∠EOF的大小为15°或165°.