题目内容
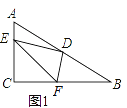
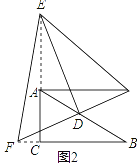
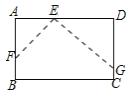
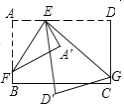
【题目】如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且![]() 在
在![]() 内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
【答案】![]()
【解析】
先根据角之间的关系表示出∠AEA′+∠DED′,再由折叠的性质得到∠A′EF+∠D′EG,然后根据∠FEG=∠A′EF+∠D′EG-∠A′ED′可表示出∠FEG,最后利用角平分线的性质求出∠FED′即可.
解:∵∠AEA′+∠DED′-∠A′ED′=180°,∠A′ED′=n°,
∴∠AEA′+∠DED′=180°+n°,
由折叠的性质可知,∠AEA′=2∠A′EF,∠DED′=2∠D′EG,
∴∠A′EF+∠D′EG=![]() ,
,
∴∠FEG=∠A′EF+∠D′EG-∠A′ED′=![]() =
=![]() ,
,
∵ED′平分∠FEG,
∴∠FED′=![]() ∠FEG=
∠FEG=![]() .
.

练习册系列答案
相关题目