题目内容
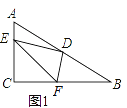
【题目】如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
(1)求证:四边形ECDC′是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
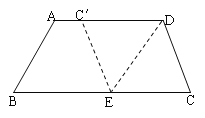
【答案】(1)见解析(2)平行四边形
【解析】
(1)由折叠性质可得CD=C′D,CE=C′E,易证CD=CE,则四边相等,可得四边形CDC′E是菱形;
(2)四边形ABED为平行四边形,由题意易证明AD=BE,又AD∥BC,四边形ABED为平行四边形.
(1)证明:依题意∠C′DE=∠CDE,CD=C′D,CE=C′E,
∵AD∥BC,
∴∠C′DE=∠DEC.
∴∠DEC=∠CDE.
∴CD=CE.
故CD=CE=C′D=C′E,四边形CDC′E是菱形.
(2)解:四边形ABED为平行四边形.
证明:∵BC=CD+AD,又CD=CE,
∴BC=CE+AD.
又BC=CE+BE,
∴AD=BE.
又AD∥BC,可得AD∥BE.
∴四边形ABED为平行四边形.

练习册系列答案
相关题目