题目内容
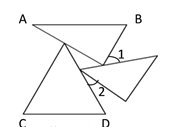
【题目】如图,平面直角坐标系中,C(0,5),D(a,5)(a >0),A、B 在 x 轴上,∠1=∠D,求证:∠ACB+∠BED=180°.

【答案】见解析
【解析】
先由C点、D点的纵坐标相等,可得CD∥x轴,即CD∥AB,然后由两直线平行同旁内角互补,可得:∠1+∠ACD=180°,然后根据等量代换可得:∠D+∠ACD=180°,然后根据同旁内角互补两直线平行,可得AC∥DE,然后由两直线平行内错角相等,可得:∠ACB=∠DEC,然后由平角的定义,可得:∠DEC+∠BED=180°,进而可得:∠ACB+∠BED=180°.
证明:∵C(0,5)、D(a,5)(a>0),
∴CD∥x轴,即CD∥AB,
∴∠1+∠ACD=180°,
∵∠1=∠D,
∴∠D+∠ACD=180°,
∴AC∥DE,
∴∠ACB=∠DEC,
∵∠DEC+∠BED=180°,
∴∠ACB+∠BED=180°.

练习册系列答案
相关题目