题目内容
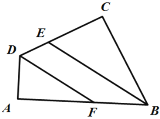
【题目】一个正三角形和一副三角板(分别含30°和45°)摆放成如图所示的位置,且AB∥CD.则∠1+∠2=__________.
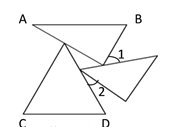
【答案】75°
【解析】
连接AC,根据平行线的性质求出∠BAC+∠ACD=180°,再由∠BAG=30°,∠ECD=60°可得出∠EAC+∠ACE的度数,根据三角形内角和定理得出∠AEC的度数,由补角的定义得出∠GEF的度数,同理可用∠1表示出∠EGF,用∠2表示出∠GFE,再由三角形内角和定理即可得出结论.
解:连接AC,
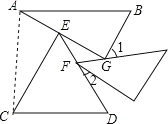
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠BAG=30°,∠ECD=60°,
∴∠EAC+∠ACE=180°-30°-60°=90°,
∵∠CED=60°,
∴∠GEF=180°-90°-60°=30°,
同理∠EGF=180°-∠1-90°=90°-∠1,∠GFE=180°-45°-∠2=135°-∠2,
∵∠GEF+∠EGF+∠GFE=180°,即30°+90°-∠1+135°-∠2=180°,解得∠1+∠2=75°.
故答案为:75°.

练习册系列答案
相关题目