题目内容
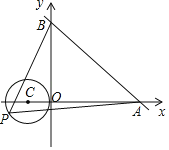
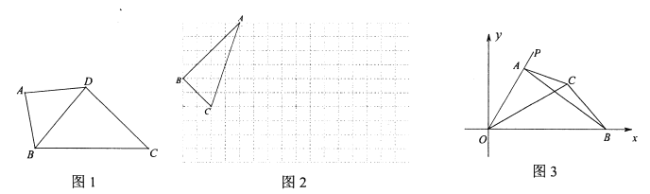
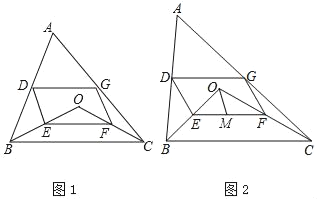
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD,
(1)求证:AD=BE;
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
【答案】(1)详见解析;(2)当△ABC满足∠ABC=90°时,四边形AECD是正方形.理由见解析.
【解析】
(1)判定△AOD≌△EOB,即可得到结论;
(2)先判定四边形ABED是菱形,可得当∠ABC=90°时,菱形ABED是正方形,据此可得结论.
(1)证明:∵AD∥BC,
∴∠CBD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
又∵AE⊥BD,
∴BO=DO,
又∵∠AOD=∠EOB,
∴△AOD≌△EOB,
∴AD=EB;
(2)当△ABC满足∠ABC=90°时,四边形AECD是正方形.理由:
∵△AOD≌△EOB,
∴AD=BE,
又∵AD∥BE,AE⊥BD,
∴四边形ABED是菱形,
∴当∠ABC=90°时,菱形ABED是正方形,
即当△ABC满足∠ABC=90°时,四边形AECD是正方形.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
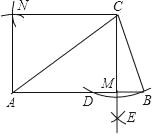
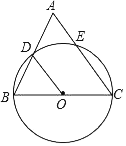
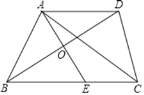
课程达标测试卷闯关100分系列答案【题目】如图1,点D、E、F、G分别为线段AB、OB、OC、AC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)如图2,若点M为EF的中点,BE:CF:DG=2:3:![]() ,求证:∠MOF=∠EFO.
,求证:∠MOF=∠EFO.
【题目】已知函数y=y1+y2,其中y1与x成反比例,y2与x﹣2成正比例,函数的自变量x的取值范围是x≥![]() ,且当x=1或x=4时,y的值均为
,且当x=1或x=4时,y的值均为![]() .
.
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探究:
①根据解析式,补全下表:
x |
| 1 |
| 2 |
| 3 | 4 | 6 | 8 | … |
y |
|
|
|
|
|
|
| … |
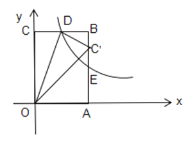
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.

(3)结合画出的函数图象,解决问题:
①当x=![]() ,
,![]() ,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
②若直线y=k与该函数图象有两个交点,则k的取值范围是 ,此时,x的取值范围是 .