题目内容
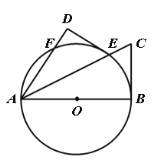
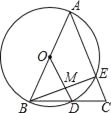
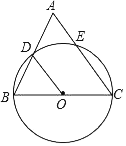
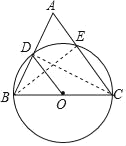
【题目】如图,在△ABC中,tanA=2,以BC为直径的⊙O分别交AB、AC于点D、点E,若D是AB的中点,OD=5,则AE=_____.
【答案】4
【解析】
根据题意可连接CD,BE,可得AC=BC=10,因为tanA=2,可得CD=2AD,在Rt△ADC中,AD2+CD2=AC2,AB=2AD=4![]() ,在Rt△AEB中,tanA=2,即可解答
,在Rt△AEB中,tanA=2,即可解答
解:连接CD,BE,
∵BC为⊙O的直径,
∴CD⊥AB,BE⊥AC,
∵D是AB的中点,
∴CD垂直平分AB,
∴AC=BC,
∵OD=5,
∴AC=BC=10,
∵tanA=2,
∴CD=2AD,
在Rt△ADC中,AD2+CD2=AC2,
即AD2+(2AD)2=102,
∴AD=2![]() ,
,
∴AB=2AD=4![]() ,
,
在Rt△AEB中,tanA=2,
∴BE=2AE,AE2+BE2=AB2,
∴AE=4,
故答案为:4

练习册系列答案
相关题目