��Ŀ����
����Ŀ�����Dz���Լ�����Խ����ഹֱ���ı��ν�����ʮ��������
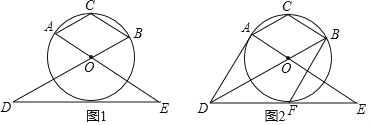
��1����ƽ���ı��Ρ����Ρ����Ρ��������У�һ������ʮ������������ ����
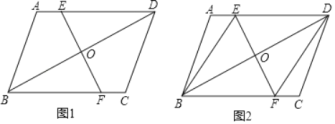
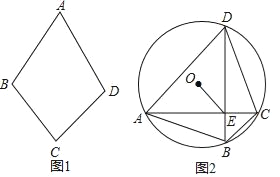
��2����ͼ1�����ı���ABCD�У�AB��AD����CB��CD
��֤�����ı���ABCD����ʮ��������
����AB��2����BAD��60�㣬��BCD��90�������ı���ABCD�������
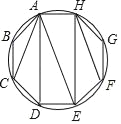
��3����ͼ2��A��B��C��D�ǰ뾶Ϊ1�ġ�O�ϰ���ʱ�뷽�����е��ĸ����㣬AC��BD���ڵ�E������ADB����CDB����ABD����CBD������AC+BD��3�����߶�OE��ȡֵ��Χ��
���𰸡���1�����Ρ������Σ���2����֤�����������ڼ�������3��![]() ��OE��
��OE��![]() ��
��
��������
��1��������ʮ�������Ķ����жϼ��ɣ�
��2��������AC��BD�����ô�ֱƽ���ߵ��ж����ɣ�
�����жϳ���ADB+��CAD=��ABD+��CAB�������жϳ���AED=��AEB=90��������AC��BD�����жϳ��ı���OMEN�Ǿ��Σ������ó�OE2=2-��AC2+BD2������AC=m���г����κ����������ɣ�
��1����ƽ���ı��Ρ����Ρ����Ρ���������ֻ�����Ρ������εĶԽ����ഹֱ��
�ʴ�Ϊ�����Ρ������Σ�
��2������ͼ1������AC��BD
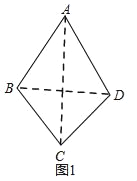
��AB��AD����CB��CD
��AC��BD�Ĵ�ֱƽ���ߣ�
��AC��BD��
���ı���ABCD����ʮ��������
����ͼ2
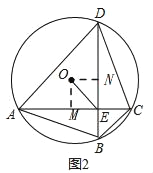
�ߡ�ADB+��CBD����ABD+��CDB����CBD����CDB����CAB��
���ADB+��CAD����ABD+��CAB��
��180������AED��180������AEB��
���AED����AEB��90����
��AC��BD��
����O��OM��AC��M��ON��BD��N������OA��OD��
��OA��OD��1��OM2��OA2��AM2��ON2��OD2��DN2��AM��![]() AC��DN��
AC��DN��![]() BD���ı���OMEN�Ǿ��Σ�
BD���ı���OMEN�Ǿ��Σ�
��ON��ME��OE2��OM2+ME2��
��OE2��OM2+ON2��2��![]() ��AC2+BD2��
��AC2+BD2��
��AC��m����BD��3��m��
�ߡ�O�İ뾶Ϊ1��AC+BD��3��
��1��m��2��
OE2��![]() ��
��
��![]() ��OE2��
��OE2��![]() ��
��
��![]() ��OE��
��OE��![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�