题目内容
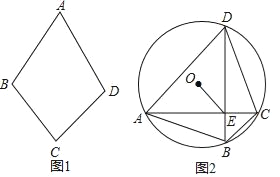
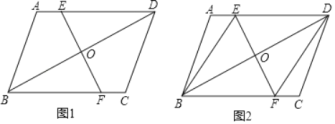
【题目】在平行四边形ABCD中,O为对角线BD的中点,EF经过点O分别交AD、BC于E、F两点,
(1)如图1,求证:AE=CF;
(2)如图2,若EF⊥BD,∠AEB=60°,请你直接写出与DE(DE除外)相等的所有线段.
【答案】(1)证明见解析;(2)BE、BF、EF、DF.
【解析】
(1)根据平行四边形的性质以及全等三角形的判定方法证明出△EOD≌△FOB,得到DE=BF,可得结论:
(2)由(1)OE=OF,而利用对角线互相垂直的平行四边形是菱形得出四边形BFDE为菱形,由∠AEB=60°可得△BEF与△BEF为等边三角形,从而得到结论.
(1)证明:![]() 四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
![]() AD//BC,AD=BC,OB=OD.
AD//BC,AD=BC,OB=OD.
![]() ∠OED=∠OFB, ∠EDO=∠FBO.
∠OED=∠OFB, ∠EDO=∠FBO.
在△EOD与△FOB中,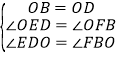 ,
,
![]() △EOD≌△FOB
△EOD≌△FOB
![]() ED=BF,
ED=BF,
又![]() AD=BC
AD=BC
![]() AE=CF.
AE=CF.
(2)由(1)得△EOD≌△FOB
![]() OE=OF,
OE=OF,
由![]() OB=OD,EF⊥BD
OB=OD,EF⊥BD
![]() 四边形BFDE为菱形,
四边形BFDE为菱形,
![]() ∠AEB=60°,
∠AEB=60°,![]() ∠BED=120°,且四边形BFDE为菱形,
∠BED=120°,且四边形BFDE为菱形,
![]() ∠BEF=∠DEF=60°,
∠BEF=∠DEF=60°, ![]() △BEF与△BEF为等边三角形,
△BEF与△BEF为等边三角形,
![]() 与DE相等的所有线段为:BE、BF、EF、DF.
与DE相等的所有线段为:BE、BF、EF、DF.

练习册系列答案
相关题目