题目内容
【题目】如图，已知A、B两点的坐标分别为A（0，2
），B（2，0），直线AB与反比例函数y＝
的图象相交于点C和点D，将△OBC绕点O逆时针方向旋转θ角（θ为锐角），得到△OB′C′，当θ＝_____时，OC′⊥AB；
【答案】60°
【解析】
设直线AB解析式为y＝kx+b，将A与B坐标代入求出k与b的值，确定出直线AB解析式，联立直线AB与反比例解析式，求出交点C坐标，过C作CM垂直于x轴，在直角三角形COM值，利用锐角三角函数定义及特殊角的三角函数值求出∠COM的度数，在直角三角形AOB中，同理求出∠ABO的度数，由外角性质即可求出∠ACO的度数；根据题意画出图形，求出OC′⊥AB时的旋转角即可确定出θ度数．
解：设直线AB的解析式为y＝kx+b，
将A（0，2
），B（2，0）代入解析式y＝kx+b中，得
，
解得：
．
∴直线AB的解析式为y＝﹣x+2，
解方程组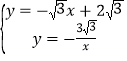
，
得：
或
，
∴点C坐标为（3，﹣），
如图，过点C作CM⊥x轴于点M，则在Rt△OMC中，CM＝，OM＝3，
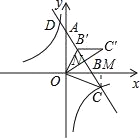
∴tan∠COM＝
＝
，
∴∠COM＝30°，
在Rt△AOB中，tan∠ABO＝
＝，
∴∠ABO＝60°，
∴∠ACO＝∠ABO﹣∠COM＝30°，
若OC′⊥AB，则有∠BNO＝90°，
∵∠NBO＝60°，
∴∠BON＝30°，
∵∠COM＝30°，
∴∠COC′＝∠COM+∠BON＝60°，即旋转角θ为60°，
故答案为：60°．
练习册系列答案
相关题目
