题目内容
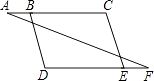
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由切线的性质可知∠DAB=90°,由直角所对的圆周为90°可知∠ACB=90°,根据同角的余角相等可知∠DAC=∠B,然后由等腰三角形的性质可知∠B=∠OCB,由对顶角的性质可知∠DCE=∠OCB,故此可知∠DAC=∠DCE;
(2)题意可知AO=1,OD=3,DC=2,由勾股定理可知AD=![]() ,由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA,故此可得到DC2=DEAD,故此可求得DE=
,由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA,故此可得到DC2=DEAD,故此可求得DE=![]() ,于是可求得AE=
,于是可求得AE=![]() .
.
试题解析:(1)∵AD是圆O的切线,∴∠DAB=90°.
∵AB是圆O的直径,∴∠ACB=90°.
∵∠DAC+∠CAB=90°,∠CAB+∠ABC=90°,∴∠DAC=∠B.
∵OC=OB,∴∠B=∠OCB.
又∵∠DCE=∠OCB,∴∠DAC=∠DCE.
(2)∵AB=2,∴AO=1.
∵sin∠D=![]() ,∴OD=3,DC=2.
,∴OD=3,DC=2.
在Rt△DAO中,由勾股定理得AD=![]() =
=![]() .
.
∵∠DAC=∠DCE,∠D=∠D,∴△DEC∽△DCA,∴![]() ,即
,即![]() .
.
解得:DE=![]() ,∴AE=AD﹣DE=
,∴AE=AD﹣DE=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目