题目内容
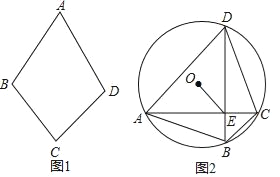
【题目】如图1,AOBC的顶点A、B、C在⊙O上,点D、E分别在BO、AO的延长线上,且OD=2OB,OE=2OA,连接DE.
(1)求∠AOB的度数;
(2)求证:DE是⊙O的切线;
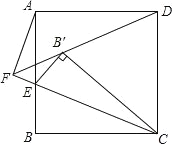
(3)如图2,设直线DE与⊙O相切于点F,连接AD、BF,判断线段AD与BF的位置关系和数量关系,并证明你的结论.
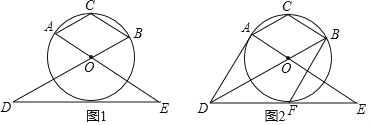
【答案】(1)120°;(2)证明见解析;(3)AD∥BF,且AD=BF.
【解析】
(1)连接OC,根据平行四边形的性质结合半径相等可得出△AOC和△BOC均为等边三角形,进而可得出∠AOC=∠BOC=60°,将其代入∠AOB=∠AOC+∠BOC中即可求出结论;(2)由(1)可知:四边形AOBC为菱形,连接CO,并延长交DE于点M,连接AB交OC于点N,由OD=2OB,OE=2OA结合对顶角相等可得出△DOE∽△BOA,根据相似三角形的性质可得出DE=2AB,OM=2ON及∠ODE=∠OBA,由内错角相等两直线平行可得出AB∥DE,由菱形的性质可得出ON⊥AB,OC=2ON,进而可得出OM⊥DE,OM=OC,再根据切线的定义即可证出DE是⊙O的切线;(3)连接AB,OF,根据切线的性质可得出OF⊥DE,结合OD=OE可得出DF=![]() DE=AB,结合AB∥DE可得出四边形ADFB为平行四边形,再利用平行四边形的性质可得出AD∥BF且AD=BF.
DE=AB,结合AB∥DE可得出四边形ADFB为平行四边形,再利用平行四边形的性质可得出AD∥BF且AD=BF.
(1)连接OC,如图3所示.
∵四边形AOBC为平行四边形,
∴AC=OB,AO=CB.
又∵OA=OC=OB,
∴△AOC和△BOC均为等边三角形,
∴∠AOC=∠BOC=60°,
∴∠AOB=∠AOC+∠BOC=120°.
(2)证明:由(1)可知:四边形AOBC为菱形.
连接CO,并延长交DE于点M,连接AB交OC于点N,如图4所示.
∵OD=2OB,OE=2OA,∠DOE=∠BOA,
∴△DOE∽△BOA,
∴DE=2AB,OM=2ON,∠ODE=∠OBA,
∴AB∥DE.
∵四边形AOBC为菱形,
∴ON⊥AB,OC=2ON,
∴OM⊥DE,OM=OC,
∴DE是⊙O的切线.
(3)解:AD∥BF,且AD=BF.
证明:在图2中,连接AB,OF,如图所示.
∵直线DE与⊙O相切于点F,
∴OF⊥DE.
∵OD=OE,
∴DF=![]() DE=AB.
DE=AB.
又∵AB∥DE,
∴四边形ADFB为平行四边形,
∴AD∥BF,且AD=BF.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案