题目内容

【题目】有一圆内接正八边形ABCDEFGH，若△ADE的面积为8，则正八边形ABCDEFGH的面积为（　　）

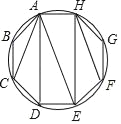
A. 32 B. 40 C. 24 D. 30

【答案】A

【解析】

取AE中点O，则点O为正八边形ABCDEFGH外接圆的圆心，连接OD，即可得△ODE的面积=×△ADE的面积，由此求得△ODE的面积，再由圆内接正八边形ABCDEFGH是由8个与△ODE全等的三角形构成，即可求得正八边形ABCDEFGH的面积.

取AE中点O，则点O为正八边形ABCDEFGH外接圆的圆心，连接OD，

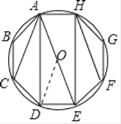
∴△ODE的面积=×△ADE的面积=×8=4，

圆内接正八边形ABCDEFGH是由8个与△ODE全等的三角形构成．

则圆内接正八边形ABCDEFGH为8×4=32，

故选A．

练习册系列答案
相关题目

【题目】某校九年级举行毕业典礼，需要从九（1）班的2名男生1名女生、九（2）的1名男生1名女生共5人中选出2名主持人．

（1）用树形图或列表法列出所有可能情形；

（2）求2名主持人来自不同班级的概率；

（3）求2名主持人恰好1男1女的概率．

【题目】如图，已知△ABC是等边三角形，点D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF，CF，连接BE并延长交CF于点G．下列结论：

①△ABE≌△ACF；②BC=DF；③S△ABC=S△ACF+S△DCF；④若BD=2DC，则GF=2EG．其中正确的结论是 ．（填写所有正确结论的序号）

【题目】已知A、B两地相距4km，上午8：00时，亮亮从A地步行到B地，8：20时芳芳从B地出发骑自行车到A地，亮亮和芳芳两人离A地的距离S（km）与亮亮所用时间t（min）之间的函数关系如图所示，芳芳到达A地时间为（ ）

A. 8：30 B. 8：35 C. 8：40 D. 8：45

【题目】如图，二次函数y＝ax2﹣4ax（a≠0）的图象与直线y＝kx+3交于点A（﹣1，）、点C两点．

（1）求a，k的值；

（2）点P在第一象限的抛物线上，其横坐标为t，连接PC、PA，设△PCA的面积为S，求S关于t的函数关系式：（直接写出t的取值范围）

（3）在（2）的条件下，作CE⊥x轴于E，点P直线y＝kx+3下方时，连接OP、BC交于D，连接ED，当∠ODE＝90°时，求t和S的值．

【题目】我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．

（1）在平行四边形、矩形、菱形、正方形中，一定是“十字形”的有　 　．

（2）如图1，在四边形ABCD中，AB＝AD，且CB＝CD

①证明：四边形ABCD是“十字形”；

②若AB＝2．∠BAD＝60°，∠BCD＝90°，求四边形ABCD的面积．

（3）如图2．A、B、C、D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，若∠ADB﹣∠CDB＝∠ABD﹣∠CBD．满足AC+BD＝3，求线段OE的取值范围．

【题目】二次函数y＝ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：①abc＞0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞﹣1时，y的值随x值的增大而增大．其中正确的结论有（　　）个．

A. 1 B. 2 C. 3 D. 4

【题目】刘帅参加“我学十九大”知识竞赛，再答对最后两道单选题就能问鼎冠军．第一道单选题有3个选项，第二道单选题有4个选项，这两道题刘帅都不会，不过刘帅还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．

（1）如果刘帅第一题不使用“求助”，那么刘帅答对第一道题的概率是　 　．

（2）从概率的角度分析，你建议刘帅在第几题使用“求助”，说明你的理由．

【题目】如图，抛物线y=+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3）．

（1）求抛物线的解析式；

（2）D是y轴正半轴上的点，OD=3，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，

①试说明EF是圆的直径；

②判断△AEF的形状，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网