题目内容
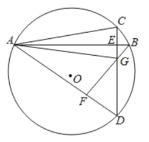
【题目】如图,CD是⊙O的切线,点C在直径AB的延长线上.
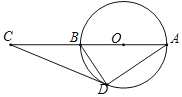
(1)求证:∠CAD=∠BDC;
(2)若BC=2,CD=3,求⊙O的半径.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,根据半径相等、切线的性质、直径所对圆周角等于180![]() ,利用等角的余角相等,即可证出;
,利用等角的余角相等,即可证出;
(2)设半径为r,在![]() 中,根据勾股定理可以求得结果.
中,根据勾股定理可以求得结果.
解:(1)如图,连接OD,
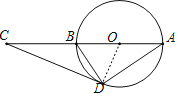
∵OB=OD,
∴∠ODB=∠ABD,
∵CD是⊙O的切线,
∴∠ODC=90°,
∴∠ODB+∠BDC=90°,
∵AB 是⊙O的直径,D为⊙O上一点,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∴∠CAD=∠BDC;
(2)设半径为r,OB=OD=r,
在![]() 中,
中,
∵BC=2,CD=3,OC2=OD2+CD2
∴![]() .
.
解得:![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目