Question

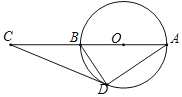
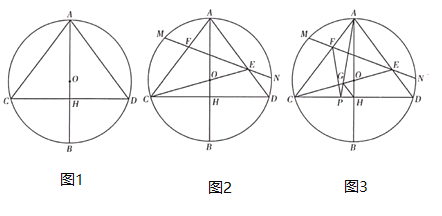
【题目】如图，AB是⊙O的直径，点C为半径OA的上的中点，CD⊥AB交⊙O于点D和点E，DF∥AB交⊙O于F，连结AF，AD．

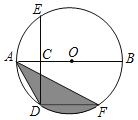
（1）求∠DAF的度数；

（2）若AB＝10，求弦AD，AF和所围成的图形的面积．（结果保留π）

Answer 1

【答案】（1）∠DAF＝30°；（2）弦AD，AF和所围成的图形的面积为π．

【解析】

（1）根据平行线的性质得到∠EDF=∠ECB=90°，求得OC=OE，于是得到结论；

（2）连接OD、OF，于是得到∠DOF=2∠DAF=60°，根据扇形的面积公式即可得到结论．

（1）∵DF∥AB，CD⊥AB，

∴∠EDF＝∠ECB＝90°，

∴AB为⊙O的直径，

∵点C为半径OA的上的中点，

∴OC＝OE，

∴∠E＝30°，

∴∠DAF＝∠E＝30°；

（2）连接OD，OF，

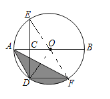
则∠DOF＝2∠E＝60°，

∵DF∥AB，

∴S△ADF＝S△DOF，

∴S阴影＝S扇形，

∵OD＝AB＝5，

∴弦AD，AF和所围成的图形的面积＝＝π．