题目内容
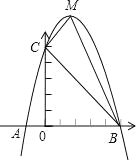
【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积
．
（3）在坐标轴上，是否存在点N，满足△BCN为直角三角形？如存在，请直接写出所有满足条件的点N．
【答案】（1）y=﹣x2+4x+5（2）15（3）存在，（0，0）或（0，﹣5）或（﹣5，0）
【解析】
试题分析：（1）把A（﹣1，0），C（0，5），（1，8）三点代入二次函数解析式，解方程组即可．
（2）先求出M、B、C的坐标，根据
即可解决问题．
（3）分三种情①C为直角顶点；②B为直角顶点；③N为直角顶点；分别求解即可．
试题解析：（1）∵二次函数y=ax2+bx+c的图象经过A（﹣1，0），C（0，5），（1，8），
则有：
，
解得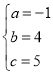
．
∴抛物线的解析式为y=﹣x2+4x+5．
（2）令y=0，得（x﹣5）（x+1）=0，x1=5，x2=﹣1，
∴B（5，0）．
由y=﹣x2+4x+5=﹣（x﹣2）2+9，得顶点M（2，9）
如图1中，作ME⊥y轴于点E，
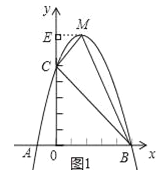
可得
=
（2+5）×9﹣
×4×2﹣
×5×5=15．
（3）存在．如图2中，
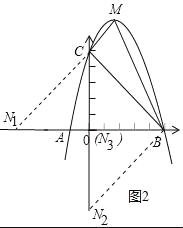
∵OC=OB=5，
∴△BOC是等腰直角三角形，
①当C为直角顶点时，N1（﹣5，0）．
②当B为直角顶点时，N2（0，﹣5）．
③当N为直角顶点时，N3（0，0）．
综上所述，满足条件的点N坐标为（0，0）或（0，﹣5）或（﹣5，0）．
练习册系列答案
阅读快车系列答案
相关题目
