Question

【题目】已知，，为正整数，．设，，，为坐标原点．若，且．

（1）求图象经过，，三点的二次函数的解析式；

（2）点是抛物线上的一动点，直线交线段于点，若，的面积，满足，求此时点的坐标．

Answer 1

【答案】（1）；（2）．

【解析】

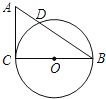
（1）由射影定理得到，即，然后代入到已知条件中得到，然后利用一元二次方程根与系数的关系求得，．利用待定系数法求二次函数解析式；

（2）由得，从而确定Q点坐标，然后利用待定系数法求得直线AQ的解析式，然后联立方程组求点D坐标．

解：（1）∵，，∴，即．

∵，

∴．

又∵

，

∴，即．

∵，，

∴，是关于的一元二次方程①的两个不相等的正整数根，

∴，解得．

又∵为正整数，故或．

当时，方程①为，没有整数解．

当时，方程①为，两根为，．

综合知：，，．

设图象经过，，三点的二次函数的解析式为，

将点的坐标代入得，解得．

∴图象经过，，三点的二次函数的解析式为．

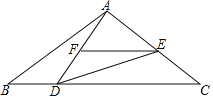
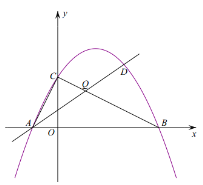
（2）如图，直线交线段于点，由，得，

∴，，∴，∵，

设直线AQ的解析式为y=kx+b

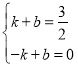可得解得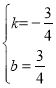

∴直线AQ的解析式为：，

联立，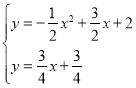

消去整理可得，，

由韦达定理：，而，

∴，∴，

∴点坐标为：．