题目内容
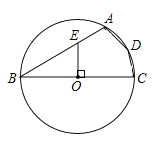
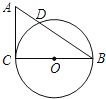
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
【答案】(1)AD=![]() ;(2)当点E是AC的中点时,ED与⊙O相切;理由见解析.
;(2)当点E是AC的中点时,ED与⊙O相切;理由见解析.
【解析】
(1)由勾股定理易求得AB的长;可连接CD,由圆周角定理知CD⊥AB,易知△ACD∽△ABC,可得关于AC、AD、AB的比例关系式,即可求出AD的长.(2)当ED与 O相切时,由切线长定理知EC=ED,则∠ECD=∠EDC,那么∠A和∠DEC就是等角的余角,由此可证得AE=DE,即E是AC的中点.在证明时,可连接OD,证OD⊥DE即可.
(1)在Rt△ACB中,∵AC=3cm,BC=4cm,∠ACB=90°,∴AB=5cm;
连接CD,∵BC为直径,
∴∠ADC=∠BDC=90°;
∵∠A=∠A,∠ADC=∠ACB,
∴Rt△ADC∽Rt△ACB;
∴![]() ,∴
,∴![]() ;
;
(2)当点E是AC的中点时,ED与⊙O相切;
证明:连接OD,

∵DE是Rt△ADC的中线;
∴ED=EC,
∴∠EDC=∠ECD;
∵OC=OD,
∴∠ODC=∠OCD;
∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°;
∴ED⊥OD,
∴ED与⊙O相切.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目