题目内容
【题目】在平面直角坐标系中 xOy 中,对于⊙C及⊙C内一点 P,给出如下定义:若存在过点 P 的直线 l,使得它与⊙C 相交所截得的弦长为![]() ,则称点 P 为⊙C的“k-近内点”.
,则称点 P 为⊙C的“k-近内点”.
(1)已知⊙O的半径为 4,
①在点中![]() ,⊙O的“4-近内点”是______________;
,⊙O的“4-近内点”是______________;
②点 P 在直线y=![]() x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
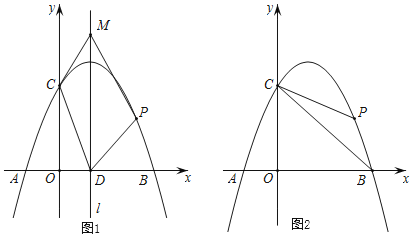
(2)⊙C的圆心为(-1,0),半径为 3,直线![]() x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2
x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2![]() -近内点”,则 b 的取值范围是____________.
-近内点”,则 b 的取值范围是____________.
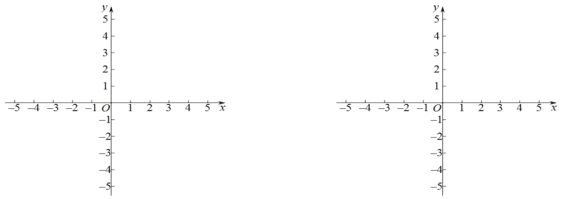
【答案】(1)①P2,P3.; ②![]() 或
或![]() ;(2)
;(2)![]() 或
或![]()
【解析】
通过读题,理解本题的实质强调两点:
(1)确定点P在圆内,即点心距小于半径.
(2)过点P的直线截圆所得的弦长可以取到k.即过圆内一点的直线截圆所得的弦的最小值应小于或等于k,数形结合,由弦长公式及其相关不等式结合来计算求解即可.
解:由于经过圆内一点的直线被圆所截的弦的长度的最大值为直径,最小值是当直线垂直于经过该点的直径时弦长最短.只有当最短的弦长不大于k值时,弦长才可能取到k.
(1)①OP1=2,r=4,由弦长公式得 最短弦长为![]() ,不满足, OP2=
,不满足, OP2=![]() ,r=4,由弦长公式得最短弦长为
,r=4,由弦长公式得最短弦长为![]() ,满足,OP3=
,满足,OP3=![]() ,r=4,由弦长公式得最短弦长
,r=4,由弦长公式得最短弦长![]() ,
,
满足,所以⊙O的“4-近内点”是P2,P3.
②依题意:设P点的坐标为![]() ,则OP2=
,则OP2=![]() ,半径r=4, 由弦长公式得最短弦长
,半径r=4, 由弦长公式得最短弦长![]() 且OP2 =
且OP2 =![]() < r2=16, 即
< r2=16, 即
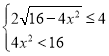
解得:![]() 或
或![]()
∵![]()
∴![]() 或
或![]() ,
,
(2)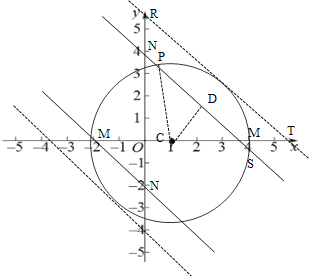
如图所示,直线MN,过圆心C作CD⊥MN,若此时弦PS=2![]() ,∴PD=
,∴PD=![]() ,
,
连接PG,则PG=3,由勾股定理得GD=2,
又∵![]() 为等腰直角三角形
为等腰直角三角形
∴GM=2![]() ,
,
∴OM=ON=2![]() +1,
+1,
由(1)可知当直线MN向上平移到RT位置恰好与圆C相切时,GT=3![]() ,
,
∴OT=OR=3![]() +1,
+1,
∴![]()
由对称性可知![]()
综上,b的取值范围为![]() 或
或![]()

 名校课堂系列答案
名校课堂系列答案【题目】我国正在逐步进入人口老龄化社会,某市老龄化社会研究机构经过抽样调查,发现当地老年人的日常休闲方式主要有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种类型,抽样调查的统计结果如下表,则下列说法不正确的是( )
五种类型,抽样调查的统计结果如下表,则下列说法不正确的是( )
休闲类型 | 休闲方式 | 人数 |
| 老年大学 |
|
| 老年合唱队 |
|
| 老年舞蹈队 |
|
| 太极拳 |
|
| 其它方式 |
|
A.当地老年人选择![]() 型休闲方式的人数最少
型休闲方式的人数最少
B.当地老年人选择![]() 型休闲方式的频率是
型休闲方式的频率是![]()
C.估计当地![]() 万名老年人中约有
万名老年人中约有![]() 万人选择
万人选择![]() 型休闲方式
型休闲方式
D.这次抽样调查的样本容量是![]()