题目内容
【题目】已知抛物线y＝x2﹣2mx+m2﹣3（m是常数）
（1）证明：无论m取什么实数，该抛物线与x轴都有两个交点．
（2）设抛物线的顶点为A，与x轴的两个交点分别为B、D，点B在点D的右侧，与y轴的交点为 C．
①若点P为△ABD的外心，求点P的坐标（用含m的式子表示）；
②当|m|≤
，m≠0时，△ABC的面积是否有最大值？如果有，请求出最大值；如果没有，请说明理由．
【答案】（1）证明见解析；（2）①P(m，-1)；②有最大值；当m＝
时，S△ABC最大＝3．
【解析】
（1）令y＝0，转化成一元二次方程，计算判别式，可得判别式的值大于0，即可得出结论；
（2）①先求出点A的坐标，再求出BD的长，进而得出BE的长，再利用勾股定理求出外接圆的半径，即可得出结论；②先求出点B的坐标，点C的坐标，分两种情况：（i）当0<m≤时，如图2，（ii）当-≤m<0时，如图3，分别得出S与m的函数关系式，即可得出结论．
（1）令y＝0，则0＝x2﹣2mx+m2﹣3，
∴△＝（﹣2m）2﹣4（m2﹣3）＝12＞0，
∴方程x2﹣2mx+m2﹣3＝0有两个不相等的实数根，
即：无论m取什么实数，该抛物线与x轴都有两个交点；
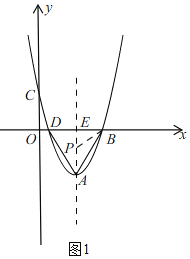
（2）①如图1，
∵抛物线y＝x2﹣2mx+m2﹣3＝（x﹣m）2﹣3，
∴A(m，﹣3)，设点D(x1，0)，B(x2，0)，
∴x1+x2＝2m，x1x2＝m2﹣3，
∴BD＝x2﹣x1＝
＝
＝2，
过点A作平行于y轴的直线，交x轴于点E，则AE⊥x轴，
∴∠AEB＝90°，
∵点A(m，﹣3)是抛物线的顶点，
∴AE＝3，BE＝
BD＝，
∴P为△ABD的外心，
∴点P在AE上，
连接BP，
设△ABD的外接圆的半径为r，则AP＝BP＝r，
∴PE＝AE﹣r＝3﹣r，
∵在Rt△BEP中， PE2+BE2＝BP2，
∴（3﹣r）2+（）2＝r2，
∴r＝2，
∴PE＝AE﹣AP＝1，
∴P(m，-1)；
②令y＝0，则x2﹣2mx+m2﹣3＝0，
∴x＝
，
∵点B在点D的右侧，
∴B(m+，0)，D(m-，0)，
令x＝0，则y＝m2﹣3，
∴C(0，m2﹣3)，
分两种情况考虑：
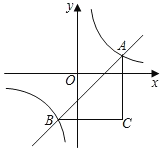
（i）当0<m≤时，如图2，
S△ABC=S梯形OCAE+S△ABES△OCB
= OE(OC+AE)+ AEBEOCOB
=m(3m2+3)+ ×3×(m+m) (3m2)(m+)
=
m2+
m
=（m +）2﹣
，
∵>0，
∴当0<m≤时，S△ABC随m的增大而增大，
∴当m=时，S△ABC取得最大值，最大值为3；
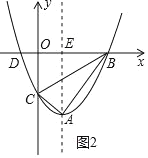
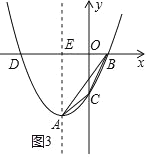
（ii）当-≤m<0时，如图3，
S△ABC=S梯形EACO+S△OCBS△ABE
=OE(OC+AE)+ OCOBAEBE
=m(3m2+3)+ (3m2)(m+) (m+m)(3m2)
=m，
∵<0，
∴当-≤m<0时，S△ABC随m的增大而减小，
∴当m=-时，S△ABC取得最大值，最大值为
．
∵3＞，
∴当m=时，△ABC的面积取得最大值，最大值为3．
