Question

【题目】如图：已知在△ABC中，AB＝AC，点D是BC上一点，∠ADE＝∠B，

（1）求证：△ABD～△DCE；

（2）点F在AD上，且＝，求证：EF∥CD．

Answer 1

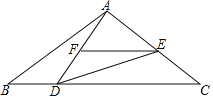
【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）由等腰三角形的性质可得∠B＝∠C，由三角形的外角性质可得∠EDC＝∠BAD，可得结论；

（2）由相似三角形的性质可得，进而推出，可证△AEF∽△ACD，可得∠AEF＝∠ACD，即EF∥CD．

证明；（1）∵AB＝AC，

∴∠B＝∠C，

∵∠ADC＝∠B+∠BAD＝∠ADE+∠CDE，且∠ADE＝∠B，

∴∠CDE＝∠BAD，且∠B＝∠C，

∴△ABD～△DCE；

（2）∵△ABD～△DCE，

∴，

∵，

∴，

∴，

∵∠EAF＝∠CAD，

∴△AEF∽△ACD，

∴∠AEF＝∠ACD，

∴EF∥CD．