题目内容
【题目】阅读材料:若x2+y2+2x-4y+5=0,求x、y.
解:∵x2+y2+2x-4y+5=0,(x2+2x+1)+(y2-4y+4)=0
∴(x+1)2+(y-2)2=0 ∴(x+1)2=0,(y-2)2=0
∴x=-1,y=2.
根据你的观察,探究下面的问题:
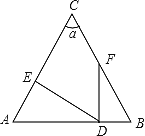
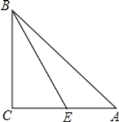
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
(1)当a、b满足a2+b216a12b+100=0,且c是不等式组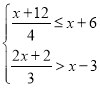 的最大整数解,试求△ABC的三边长;
的最大整数解,试求△ABC的三边长;
(2)在(1)的条件得到满足的△ABC中,若设AE=m,则当m满足什么条件时,BE将△ABC的周长分成两部分的差不小于2?
【答案】(1)a=8,b=6,c=10;(2)m≥3或m≤1.
【解析】
(1)根据a2+b2-16a-12b+100=0,且c是不等式组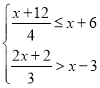 的最大整数解,可以分别求得a、b、c的值;
的最大整数解,可以分别求得a、b、c的值;
(2)由题意可得|(AB+AE)-(BC+CE)|≥2,可以得到关于m的不等式,从而可以解答本题.
(1)∵a2+b2-16a-12b+100=0,
∴(a-8)2+(b-6)2=0,
∴a-8=0,b-6=0,
得a=8,b=6,
解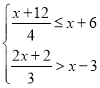 得,-4≤x<11,
得,-4≤x<11,
∵c是不等式组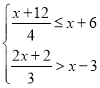 的最大整数解,
的最大整数解,
∴c=10,
∴a=8,b=8,c=10;
(2)由题意可得,
|(AB+AE)-(BC+CE)|≥2,
即|(10+m)-(8+6-m)|≥2,
解得,m≥3或m≤1,
即当m≥3或m≤1时,BE分△ABC的周长的差不小于2.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目