题目内容
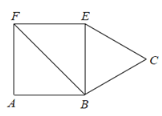
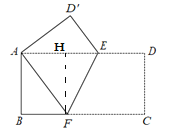
【题目】如图,把一张长方形纸片 ABCD 折叠起来,使其对角顶点 A,C 重合,若其长 BC 为 9,宽 AB 为 3.
⑴求证:△AEF 是等腰三角形;
⑵EF= .
【答案】(1)见详解;(2)![]()
【解析】
(1) 由折叠可知,∠EFC=∠AFE,根据AD∥BC,得到∠AEF=∠EFC,可得∠AEF=∠AFE,即可得出结论;
(2)过点F作FH⊥AD,设BF=x,则AF=CF=9x,求出x的值,再根据勾股定理即可得出EF=![]() =
=![]() .
.
(1)证明:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠AEF=∠EFC.
由折叠可知,∠EFC=∠AFE,
∴∠AEF=∠AFE.
∴AE=AF.
∴△AEF是等腰三角形.
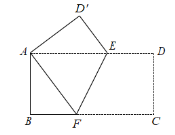
(2)解:如图,过点F作FH⊥AD,
设BF=x,
则AF=CF=9x,
在Rt△ABF中,由BF2+AB2=AF2可得x2+32=(9x)2,
解得:x=4,
∴AF=FC=9-4=5,
∴AE=AF=5,
∵四边形ABFH是矩形,
∴AH=BF=4,AB=HF=3
∴HE=AE-AH=1,
∴EF=![]() =
=![]() =
=![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
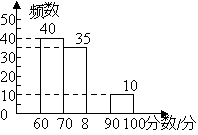
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如下:
频率分布统计表 | 频率分布直方图 | ||
分数段 | 频数 | 频率 |
|
60≤x<70 | 40 | 0.40 | |
70≤x<80 | 35 | b | |
80≤x<90 | a | 0.15 | |
90≤x<100 | 10 | 0.10 | |
请根据上述信息,解答下列问题:
(1)表中:a= ,b= ;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数。