题目内容
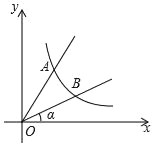
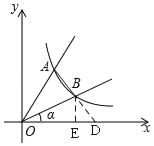
【题目】如图,直线y=2x与反比例函数y=![]() (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=![]() .
.
(1)求k的值及点B坐标.
(2)连接AB,求三角形AOB的面积S△AOB.
【答案】 (1)k=2 B(2,1)(2)![]()
【解析】分析:(1)把点A(1,a)代入直线y=2x,求出a=2,再把A(1,2)代入y=![]() ,即可求出k的值;过点B作BC⊥x轴于点C,在RT△BOC中,由tanα=
,即可求出k的值;过点B作BC⊥x轴于点C,在RT△BOC中,由tanα=![]() ,可设B(2h,h),将 B(2h,h) 代入y=
,可设B(2h,h),将 B(2h,h) 代入y=![]() ,求出h的值,即可求解;(2)由A(1,2),B(2,1).利用待定系数法求出直线AB的解析式为y=-x+3,那么直线AB与x轴交点D的坐标为(3,0),根据差可求得△AOB的值.
,求出h的值,即可求解;(2)由A(1,2),B(2,1).利用待定系数法求出直线AB的解析式为y=-x+3,那么直线AB与x轴交点D的坐标为(3,0),根据差可求得△AOB的值.
详解:(1)把点A(1,a)代入y=2x,
得a=2,
则A(1,2).
把A(1,2)代入y=![]() ,得k=1×2=2;
,得k=1×2=2;
过B作BC⊥x轴于点C.
∵在Rt△BOC中,tanα=![]() ,
,
∴可设B(2h,h).
∵B(2h,h)在反比例函数y=![]() 的图象上,
的图象上,
∴2h2=2,解得h=±1,
∵h>0,
∴h=1,
∴B(2,1);
(2)∵A(1,2),B(2,1),
∴直线AB的解析式为y=﹣x+3,
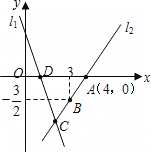
设直线AB与x轴交于点D,则D(3,0),
∵S△AOB=S△ABD﹣S△OBD=![]() ODyA﹣
ODyA﹣![]() ODyB,
ODyB,
=![]() ×3×2﹣
×3×2﹣![]() ×3×1,
×3×1,
=3﹣![]() ,
,
=![]() .
.

【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]()
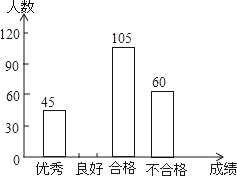
【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.