题目内容
写出下列命题的已知、求证,并完成证明过程.

命题:如果平行四边形的一条对角线平分它的一个内角,那么这个平行四边形是菱形.
已知:如图, .
求证: .
证明: .

命题:如果平行四边形的一条对角线平分它的一个内角,那么这个平行四边形是菱形.
已知:如图, .
求证: .
证明: .
在□ABCD中,对角线AC平分∠DAB(或∠DCB).
□ABCD是菱形.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠BCA
∵对角线AC平分∠DAB,
∴∠DAC=∠BAC.
∴∠BCA=∠BAC.
∴BA=BC
∴□ABCD是菱形.
□ABCD是菱形.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠BCA
∵对角线AC平分∠DAB,
∴∠DAC=∠BAC.
∴∠BCA=∠BAC.
∴BA=BC
∴□ABCD是菱形.
试题分析:把原命题的题设作为已知,把原命题的结论作为求证即可,再根据根据一条对角线平分一个内角,则有这两个角相等.根据两直线平行内错角相等,得出一个三角形两个内角相等,即两边相等,根据菱形的概念:有一组邻边相等的平行四边形是菱形即证.
已知:如图,在□ABCD中,对角线AC平分∠DAB(或∠DCB).
求证:□ABCD是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠BCA
∵对角线AC平分∠DAB,
∴∠DAC=∠BAC.
∴∠BCA=∠BAC.
∴BA=BC
∴□ABCD是菱形.
点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
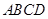 的对角线
的对角线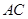 、
、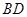 的长分别为12cm、16cm,
的长分别为12cm、16cm,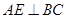 于点
于点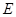 ,则
,则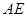 的长是_________cm.
的长是_________cm.
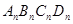 的面积为 .
的面积为 .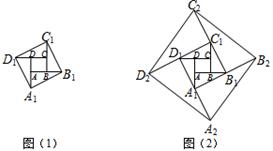
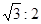 ;⑤△DEC与△ABE的面积比为
;⑤△DEC与△ABE的面积比为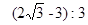 。则以上结论正确的是 .(只填正确结论的序号)
。则以上结论正确的是 .(只填正确结论的序号)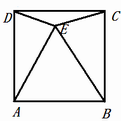

 CH.
CH.