题目内容
已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G. DH平分∠ADE交CF于点H,连接BH.

(1)若DG=2,求DH的长;
(2)求证:BH+DH=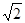 CH.
CH.

(1)若DG=2,求DH的长;
(2)求证:BH+DH=
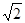 CH.
CH.(1)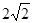 (2)证明DM=BH,DM+DH=
(2)证明DM=BH,DM+DH=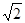 CH所以BH+DH=
CH所以BH+DH=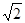 CH
CH
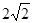 (2)证明DM=BH,DM+DH=
(2)证明DM=BH,DM+DH=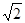 CH所以BH+DH=
CH所以BH+DH=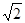 CH
CH试题分析:(1)∵DG⊥CF且DF=CD
∴∠FDG=
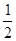 ∠FDC
∠FDC ∵DH平分∠ADE
∴∠FDH=
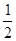 ∠ADF 2分
∠ADF 2分∴∠HDG=∠FDG-∠FDH=
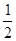 ∠FDC-
∠FDC-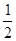 ∠ADF
∠ADF=
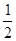 (∠FDC-∠ADF)=
(∠FDC-∠ADF)=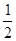 ∠ADC=45°
∠ADC=45° ∴△DGH为等腰直角三角形
∵DG=2,
∴DH=
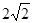 .
.(2)过点C作CM⊥CH, 交HD延长线于点M
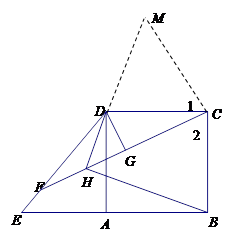
∵∠1+∠DCH=∠2+∠DCH=900
∴∠1=∠2
又△DGH为等腰直角三角形
∴△MCH为等腰直角三角形
∴MC=HC
又∵四边形ABCD为正方形
∴CD=CB
∴△MCD≌△HCB
∴DM=BH
又∵△MCH为等腰直角三角形
∴DM+DH=
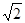 CH
CH∴BH+DH=
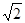 CH
CH 点评:本题考查角平分线,全等三角形,解本题的关键是掌握角平分线的性质,熟悉全等三角形的判定方法,会证明三角形全等

练习册系列答案
相关题目



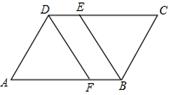
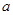 ,且
,且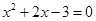 的根,则□ABCD的周长为( )
的根,则□ABCD的周长为( )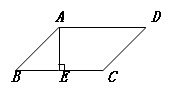



 的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,
的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,  的平分线分别交AF、AD于点G、H.
的平分线分别交AF、AD于点G、H.
 ,
, ,求
,求 的长度;
的长度; .
.