题目内容
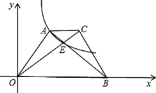
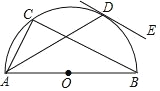
【题目】如图,在△ABC中,AB=AC,∠ABC=72°,BD、CE分别是△ABC、△BCD的角平分线.则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
【答案】A
【解析】
根据等腰三角形的定义即可找到一个等腰三角形,然后利用等边对等角、三角形的内角和、角平分线的定义求出图中各个角的度数,再根据等角对等边即可找出所有的等腰三角形.
解:∵AB=AC,∠ABC=72°,
∴∠ABC=∠ACB=72°,△ABC为等腰三角形
∴∠A=180°-∠ABC-∠ACB=36°
∵BD平分∠ABC
∴∠ABD=∠CBD=![]() =36°
=36°
∴∠ABD=∠A=36°,∠BDC=180°-∠ACB-∠CBD=72°
∴DA=DB,即△DAB为等腰三角形,∠BDC=∠ACB=72°
∴BD=BC,即△BDC为等腰三角形
∵CE平分∠BCD
∴∠BCE =∠DCE=![]() =36°
=36°
∴∠BCE=∠CBD=36°,∠CED=180°-∠DCE-∠BDC=72°
∴EB=EC,即△EBC为等腰三角形,∠CED=∠BDC=72°
∴CE=CD,即△CDE为等腰三角形,共有5个等腰三角形
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目