题目内容
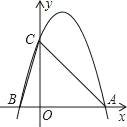
【题目】如图所示，二次函数y=﹣2x2+4x+m的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．
(1)求m的值及点B的坐标；
(2)求△ABC的面积；
(3)该二次函数图象上有一点D（x，y），使S△ABD=S△ABC，请求出D点的坐标．
【答案】（1）（﹣1，0）；（2）12（3）（2，6）、（1+
，﹣6）、（1﹣，﹣6）
【解析】
试题（1）先把点A坐标代入解析式，求出m的值，令y=0，进而求出点B的坐标；
（2）根据二次函数的解析式求出点C的坐标，从而求出△ABC的面积；
（3）根据S△ABD=S△ABC求出点D纵坐标的绝对值，然后分类讨论，求出点D的坐标．
试题解析：（1）∵函数过A（3，0），∴﹣18+12+m=0，∴m=6，∴该函数解析式为：y=﹣2x2+4x+6，∴当﹣2x2+4x+6=0时，x1=﹣1，x2=3，∴点B的坐标为（﹣1，0）；
（2）C点坐标为（0，6），S△ABC=
=12；
（3）∵S△ABD=S△ABC=12，∴S△ABD=
=12，∴|y|=±6，
①当y=6时：﹣2x2+4x+6=6，解得：x1=0，x2=2，∴D点坐标为（2，6），
②当y=﹣6时：﹣2x2+4x+6=﹣6，解得：x1=1+
，x2=1﹣
∴D点坐标为（1+，﹣6）、（1﹣，﹣6）
综上，D点坐标为（2，6）、（1+，﹣6）、（1﹣，﹣6）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
