题目内容
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
【答案】(1)![]() ;(2)BC-AC=2;(3)点Q的坐标为(
;(2)BC-AC=2;(3)点Q的坐标为(![]() )或(
)或(![]() ).
).
【解析】试题分析:(1)由抛物线![]() 经过点(2,3),对称轴为直线x =1,利用待定系数法即可得;
经过点(2,3),对称轴为直线x =1,利用待定系数法即可得;
(2)如图,设l与对称轴交于点M,根据抛物线的对称性,可知AM=BM, AM=AC+CM,BC=BM+CM,推导即可得;
(3)由OP=OQ可知P、Q两点关于x轴对称,求出平移后的解析式,表示出P、Q的坐标,根据关于x轴对称的点的性质即可求得 .
试题解析:(1)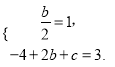 ,解得
,解得![]() ,
,
∴![]() ;
;
(2)如图,设l与对称轴交于点M,则有CM=1,
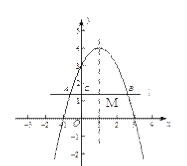
由抛物线的对称性可得,BM= AM,
又∵BC=BM+CM, AM=AC+CM,
∴BC-AC= BM+MC-AC= AM+MC-AC= AC+CM+MC-AC=2CM=2;
(3)![]() =-(x-1)2+4,
=-(x-1)2+4,
所以平移后的抛物线解析式为: ![]() -4=-x2+2x-1,
-4=-x2+2x-1,
设P(m,-m2+2m+3),则平移后对应点Q(m,-m2+2m-1),
因为OP=OQ,所以P、Q两点关于x轴对称,
所以:(-m2+2m+3)+(-m2+2m-1)=0,
解得:m1=![]() ,m2=
,m2=![]() ,
,
所以:点Q的坐标为(![]() )或(
)或(![]() ).
).

练习册系列答案
相关题目