题目内容
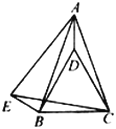
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 内,
内,![]() ,
,![]() ,点
,点![]() 在
在![]() 外,
外,![]() ,
,![]() .
.
(1)求![]() 的度数.
的度数.
(2)判断![]() 的形状并加以证明.
的形状并加以证明.
(3)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)∠ADC=150°;(2)△ACE是等边三角形,证明见解析;(3)DE=6.
【解析】
(1)先证明△DBC是等边三角形,根据SSS证得△ADC≌△ADB,得到∠ADC=∠ADB即可得到答案;
(2)证明△ACD≌△ECB得到AC=EC,利用![]() 即可证得
即可证得![]() 的形状;
的形状;
(3)根据![]() 及等边三角形的性质求出∠EDB=30°,利用
及等边三角形的性质求出∠EDB=30°,利用![]() 求出∠DBE=90°,根据△ACD≌△ECB,AD=3,即可求出DE的长.
求出∠DBE=90°,根据△ACD≌△ECB,AD=3,即可求出DE的长.
(1)∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形.
∴DB=DC,∠BDC=∠DBC=∠DCB=60°.
在△ADB和△ADC中,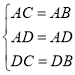 ,
,
∴△ADC≌△ADB.
∴∠ADC=∠ADB.
∴∠ADC=![]() (360°﹣60°)=150°.
(360°﹣60°)=150°.
(2)△ACE是等边三角形.
理由如下:∵∠ACE=∠DCB =60°,
∴∠ACD=∠ECB.
∵∠CBE=150°,∠ADC=150°
∴∠ADC=∠EBC.
在△ACD和△ECB中, ,
,
∴△ACD≌△ECB.
∴AC=CE.
∵∠ACE=60°,
∴△ACE是等边三角形.
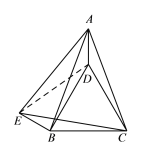
(3)连接DE.
∵DE⊥CD,
∴∠EDC=90°.
∵∠BDC=60°,
∴∠EDB=30°.
∵∠CBE=150°,∠DBC=60°,∴∠DBE=90°.
∴EB=![]() DE.
DE.
∵△ACD≌△ECB,AD=3,
∴EB = AD =3.
∴DE=2EB=6.

练习册系列答案
相关题目