题目内容
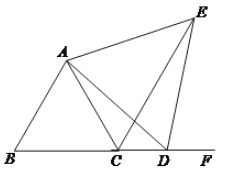
【题目】如图, △ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
1.求证:△CAE≌△BAD;
2.判断直线AB与EC的位置关系,并说明理由.
【答案】(1)见解析;(2)EC∥AB,理由见解析.
【解析】
(1)根据△ADE与△ABC都是等边三角形,得到AC=AB,AE=AD,∠DAE=∠BAC=60°,从而得到∠DAE+∠CAD=∠BAC+∠CAD、即∠CAE=∠BAD,利用SAS证得△CAE≌△BAD;
(2)由△CAE≌△BAD,得到∠ACE=∠B=60°,∠ACE=∠BAC=60°,利用内错角相等证得EC∥AB.
(1)∵△ADE与△ABC都是等边三角形,
∴ AC = AB,AE = AD,∠DAE =∠BAC =60°.
∴ ∠DAE+∠CAD =∠BAC+∠CAD. 即∠CAE =∠BAD.
∴在△CAE与△BAD中,
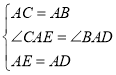
∴ △CAE≌△BAD.
(2)EC∥AB.
由△CAE≌△BAD,
∴∠ACE=∠B=60°,
∴∠ACE=∠BAC=60°,
∴EC∥AB.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目