题目内容
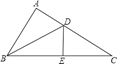
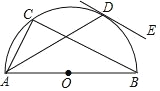
【题目】如图,△ABC 内接于半⊙O,AB 为直径,弦 AD 平分∠CAB,DE 切⊙O 于点 D.
(1) 求证:DE∥BC
(2) 若 AD=BC,⊙O 半径为 2,求∠CAD 与弧CD围成区域的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OD.只要证明DE⊥OD,BC⊥OD即可解决问题;
(2)只要证明△COD是等边三角形,可得∠CDO=∠DOB=60°,推出CD∥AB,推出S△ACD=S△COD,可得∠CAD与![]() 围成区域的面积=扇形OCD的面积,由此即可解决问题.
围成区域的面积=扇形OCD的面积,由此即可解决问题.
(1)证明:连接OD.
∵DE是⊙O切线,
∴OD⊥DE,
∵AD平分∠CAB,
∴∠DAC=∠DAB,
∴![]() =
=![]() ,
,
∴OD⊥BC,
∴DE∥BC.
(2)∵AD=BC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,∵
,∵![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴∠CDO=∠DOB=60°,
∴CD∥AB,
∴S△ACD=S△COD,
∴∠CAD与![]() 围成区域的面积=扇形OCD的面积=
围成区域的面积=扇形OCD的面积=![]() =
=![]() π.
π.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目