题目内容
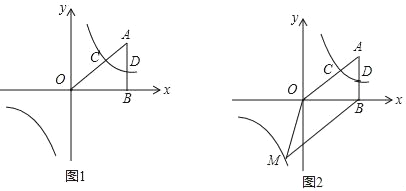
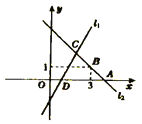
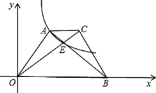
【题目】如图,梯形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点,若AC : OB = 1:3,梯形AOBC面积为24,则k =( )
(k>0)经过A、E两点,若AC : OB = 1:3,梯形AOBC面积为24,则k =( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
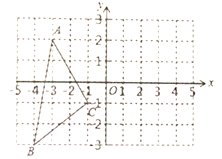
设△ACE的面积为S,则可得出△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,从而求出S.过点E作EF⊥OB,过点A作AM⊥OB于点M,设△OAM的面积为a,则△OEF的面积也为a,利用△BEF∽△BAM可得出a的值,即△OEF的面积,则可求出k的值.
解:∵四边形AOBC是梯形,AC∥OB,AC:OB=1:3,
∴CE:EO=1:3,AE:EB=1:3,
设△ACE的面积为S,则△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,
又∵梯形AOBC面积为24,
∴S+9S+3S+3S=24,
解得S=![]() .
.
过点E作EF⊥OB,过点A作AM⊥OB于点M,

设△OAM的面积为a,则△OEF的面积也为a,则△AMB的面积=18-a,△EFB的面积为![]() .
.
∵EF∥AM,
∴△AMB∽△EFB,
∴![]() ,
,
解得a=![]() ,则k=
,则k=![]() ,
,
故选择C.

练习册系列答案
相关题目