ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥÷÷–ΆΚ≈ΒΡΈ¬ΩΊΥ°œδΒΡΙΛΉςΙΐ≥Χ «ΘΚΫ”Ά®Βγ‘¥ΚσΘ§‘Ύ≥θ ΦΈ¬Ε»20Γφœ¬Φ”»»Υ°œδ÷–ΒΡΥ°ΘΜΒ±Υ°Έ¬¥οΒΫ…ηΕ®Έ¬Ε»80Γφ ±Θ§Φ”»»ΆΘ÷ΙΘΜ¥ΥΚσΥ°œδ÷–ΒΡΥ°Έ¬ΩΣ Φ÷πΫΞœ¬ΫΒΘ§Β±œ¬ΫΒΒΫ20Γφ ±Θ§‘Ό¥ΈΉ‘Ε·Φ”»»Υ°œδ÷–ΒΡΥ°÷Ν80Γφ ±Θ§Φ”»»ΆΘ÷ΙΘΜΒ±Υ°œδ÷–ΒΡΥ°Έ¬œ¬ΫΒΒΫ20Γφ ±Θ§‘Ό¥ΈΉ‘Ε·Φ”»»Θ§Γ≠Θ§Α¥’’“‘…œΖΫ Ϋ≤ΜΕœ―≠ΜΖΘ°
–ΓΟςΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘ΗΟ–ΆΚ≈Έ¬ΩΊΥ°œδ÷–ΒΡΥ°Έ¬Υφ ±Φδ±δΜ·ΒΡΙφ¬…Ϋχ––ΝΥΧΫΨΩΘ°ΖΔœ÷Υ°Έ¬y « ±ΦδxΒΡΚ· ΐΘ§Τδ÷–yΘ®ΒΞΈΜΘΚΓφΘ©±μ ΨΥ°œδ÷–Υ°ΒΡΈ¬Ε»Θ°xΘ®ΒΞΈΜΘΚminΘ©±μ ΨΫ”Ά®Βγ‘¥ΚσΒΡ ±ΦδΘ°
œ¬Οφ «–ΓΟςΒΡΧΫΨΩΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
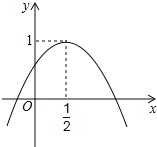
Θ®1Θ©œ¬±μΦ«¬ΦΝΥ32minΡΎ14Ηω ±ΦδΒψΒΡΈ¬ΩΊΥ°œδ÷–Υ°ΒΡΈ¬Ε»yΥφ ±ΦδxΒΡ±δΜ·«ιΩω
Ϋ”Ά®Βγ‘¥ΚσΒΡ ±ΦδxΘ®ΒΞΈΜΘΚminΘ© | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | Γ≠ |
Υ°œδ÷–Υ°ΒΡΈ¬Ε»yΘ®ΒΞΈΜΘΚΓφΘ© | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | Γ≠ |
mΒΡ÷ΒΈΣ ΘΜ
Θ®2Θ©ΔΌΒ±0ΓήxΓή4 ±Θ§–¥≥ω“ΜΗωΖϊΚœ±μ÷– ΐΨίΒΡΚ· ΐΫβΈω Ϋ ΘΜ
Β±4ΘΦxΓή16 ±Θ§–¥≥ω“ΜΗωΖϊΚœ±μ÷– ΐΨίΒΡΚ· ΐΫβΈω Ϋ ΘΜ
ΔΎ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Οη≥ωΝΥ…œ±μ÷–≤ΩΖ÷ ΐΨίΕ‘”ΠΒΡΒψΘ§ΗυΨίΟη≥ωΒΡΒψΘ§Μ≠≥ωΒ±0ΓήxΓή32 ±Θ§Έ¬Ε»yΥφ ±Φδx±δΜ·ΒΡΚ· ΐΆΦœσΘΚ
Θ®3Θ©»γΙϊΥ°Έ¬yΥφ ±ΦδxΒΡ±δΜ·Ιφ¬…≤Μ±δΘ§‘Λ≤βΥ°Έ¬ΒΎ8¥Έ¥οΒΫ40Γφ ±Θ§ΨύάκΫ”Ά®Βγ‘¥ minΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©50ΘΜΘ®2Θ©ΔΌy=15x+20Θ§y=![]() ΘΜΔΎΆΦœσΦϊΫβΈωΘΜΘ®3Θ©56.
ΘΜΔΎΆΦœσΦϊΫβΈωΘΜΘ®3Θ©56.
ΓΨΫβΈωΓΩ
Θ®1Θ©Ιέ≤λ±μΗώΘ§Ω…ΒΟΟΩΖ÷÷”…œ…ΐΕύ…ΌΈ¬Ε»Θ§”…¥ΥΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©ΔΌΙΊœΒ±μΗώΘ§Ω…÷ΣΚ· ΐ «“Μ¥ΈΚ· ΐΘ§”…¥Υάϊ”Ο¥ΐΕ®œΒ ΐΖ®ΫβΨωΈ ΧβΘ°
ΔΎΙΊœΒ±μΗώΩ…÷ΣΘ§Κ· ΐΖ¥±»άΐΚ· ΐΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®3Θ©ΗυΨί±μΗώΘ§άϊ”ΟΟηΒψΖ®Μ≠≥ωΆΦœσΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®4Θ©άϊ”ΟΆΦœσ―Α’“Ιφ¬…Φ¥Ω…ΫβΨωΘ°
Θ®1Θ©”…Χβ“βΩ…÷Σ2Ζ÷÷”Έ¬Ε»…œ…ΐ30ΓφΘ§Υυ“‘m=50Θ§
Ι ¥πΑΗΈΣ50Θ°
Θ®2Θ©ΔΌΒ±0ΓήxΓή4 ±Θ§Κ· ΐΫβΈω Ϋ «“Μ¥ΈΚ· ΐΘ§y=15x+20Θ°
ΔΎΒ±4ΘΦxΓή16 ±Θ§Κ· ΐΫβΈω Ϋ «Ζ¥±»άΐΚ· ΐy=![]() Θ°
Θ°
Ι ¥πΑΗΈΣy=15x+20Θ§y=![]() Θ°
Θ°
Θ®3Θ©Κ· ΐΆΦœσ»γΆΦΥυ ΨΘ§
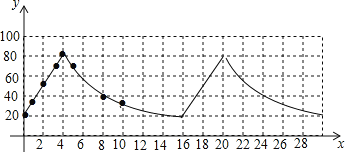
Θ®4Θ©Ιέ≤λΆΦœσΩ…÷Σ‘Λ≤βΥ°Έ¬ΒΎ8¥Έ¥οΒΫ40Γφ ±Θ§ΨύάκΫ”Ά®Βγ‘¥56minΘ°
Ι ¥πΑΗΈΣ56Θ°