题目内容
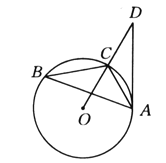
【题目】已知:点A,B,C都在⊙O上,连接AB,AC,点D,E分别在AC,AB上,连接CE并延长交⊙O于点F,连接BD,BF,∠BDC﹣∠BFC=2∠ABF.
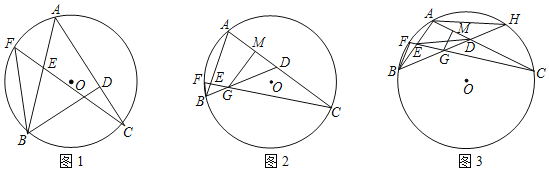
(1)如图1,求证:∠ABD=2∠ACF;
(2)如图2,CE交BD于点G,过点G作GM⊥AC于点M,若AM=MD,求证:AE=GD;
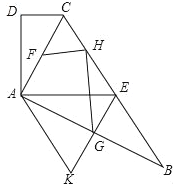
(3)如图3,在(2)的条件下,当AE:BE=8:7时,连接DE,且∠ADE=30°.延长BD交⊙O于点H,连接AH,AH=8![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)13
【解析】
(1)注意到同弧所对的圆周角相等以及∠BDC是△ABD的外角,结合题中所告诉的角度等式进行代换变形即可得结论;
(2)连接AG,设∠CGD=∠BGE=β,∠ACF=α,然后推出∠AEG=∠AGE,再根据等角对等边即可证出结论;
(3)首先注意到特殊角∠ADE=30°,于是作AP⊥DE于P,由HL定理可得△AEP≌△AGM,进而推出△AEG是等边三角形,设AE=8k,BE=7k,作GN⊥AE于N,解△BGN可得sin∠ABG的值,而∠ABG是圆周角且所对的弦为AH,于是连接AO并延长交圆O于Q,连接HQ,sin∠AQH=sin∠ABG=![]() ,而AH已知,从而求出直径AQ,半径也就自然知道了.
,而AH已知,从而求出直径AQ,半径也就自然知道了.
解:(1)∵∠BDC=∠ABD+∠BAC,
∠BDC﹣∠BFC=2∠ABF,
∴∠ABD+∠BAC﹣∠BFC=2∠ABF,
∵∠ABF=∠ACF,∠BFC=∠BAC,
∴∠ABD+∠BFC﹣∠BFC=2∠ACF,
∴∠ABD=2∠ACF.
(2)如图2,连接AG.
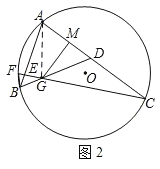
设∠CGD=∠BGE=β,∠ACF=α,
则∠ABD=2α,∠AEG=∠ABD+∠BGE=2α+β,
∠GDA=∠CGD+∠ACF=α+β,
∵GM⊥AD于M且AM=DM,
∴AG=DG,
∴∠GAD=∠GDA=α+β,
∴∠AGE=∠GAD+∠ACF=α+β+α=2α+β,
∴∠AGE=∠AEG,
∴AE=AG=GD.
(3)如图3,连接AG,作AP⊥DE于P,
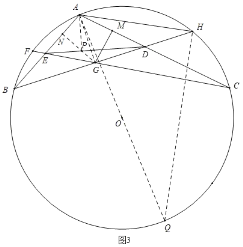
∵∠ADE=30°,
∴∠PAD=60°,AP=![]() AD,
AD,
∵GM⊥AD,
∴∠AMG=∠APE=90°,
∵AM=MD,
∴AM=![]() AD=AP,
AD=AP,
由(2)可知AE=AG,
在Rt△AEP和Rt△AGM中:
![]()
∴Rt△AEP≌Rt△AGM(HL),
∴∠EAP=∠GAM,
∵∠GAM+∠PAG=∠PAD=60°,
∴∠EAP+∠PAG=∠EAG=60°,
∴△AEG是等边三角形,
∴EG=AE=AG=DG,
∵AE:BE=8:7,
∴设AE=8k,BE=7k,
作GN⊥AE于N,AN=EN=4k,NG=4![]() k,
k,
∴BN=BE+EN=11k,
∴BG=![]() =
=![]() =13k,
=13k,
∴sin∠ABG=![]() =
=![]() ,
,
连接AO并延长交圆O于Q,连接HQ,
则AQ为直径,∠AHQ=90°,
∴sin∠AQH=![]() ,
,
∵∠AQH=∠ABG,AH=8![]() ,
,
∴![]() =
=![]() ,
,
∴AQ=26,
∴AO=![]() AQ=13,
AQ=13,
即⊙O的半径为13.

 千里马走向假期期末仿真试卷寒假系列答案
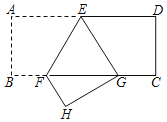
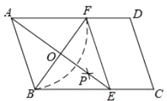
千里马走向假期期末仿真试卷寒假系列答案【题目】如图,平行四边形ABCD中,O是对角线BD的中点,过点O的直线EF分别交DA,BC的延长线于E,F.
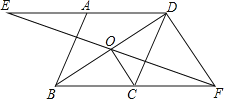
(1)求证:AE=CF;
(2)若AE=BC,试探究线段OC与线段DF之间的关系,并说明理由.
【题目】某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x(单位:min) | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y(单位:℃) | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为 ;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式 ;
当4<x≤16时,写出一个符合表中数据的函数解析式 ;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源 min.